Примеры решения систем линейных уравнений методом Крамера

 

 

Пример 1

 

   

                      .

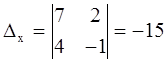
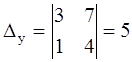
  Проверка:

                               Ответ: (3; -1).

 

Пример 2

                     

  

Проверка:

                    Ответ: x=0,5; y=2; z=1,5.

 

 

           

 

Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

       Итак, пусть дана система, содержащая m линейных уравнений с п неизвестными:

                               а₁₁х₁ + а₁₂х₂ + …+ а_1nх_n = b₁;

                               а₂₁х₁ + а₂₂х₂ + …+ а_2nх_n = b₂;                    

_.                                    ……………………………………

                              а_m1х₁ + а_m2х₂ + …+ а_mnх_n = b_m

       Метод Гаусса решения системы заключается в последовательном исключении переменных.

Схема единственного деления. Рассмотрим простейший вариант метода Гаусса, называемый схемой единственного деления.

Прямой ход состоит из n - 1 шагов исключения.

1-й шаг. Целью этого шага является исключение неизвестного x ₁ из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a ₁₁ ¹ 0. Будем называть его главным элементом 1- го шага.

Найдем величины

q_{i 1} = a_{i 1}/ a ₁₁ (i = 2, 3, …, n),

называемые множителями 1- го шага. Вычтем последовательно из второго, третьего, …, n- го уравнений системы первое уравнение, умноженное соответственно на q_{2 1}, q ₃₁, …, q_{n 1}. Это позволит обратить в нуль коэффициенты при x ₁ во всех уравнениях, кроме первого. В результате получим эквивалентную систему

a ₁₁ x ₁ + a ₁₂ x ₂ + a ₁₃ x ₃ + … + a _{1 n}x_n = b ₁ ,

a ₂₂⁽¹⁾ x ₂ + a ₂₃⁽¹⁾ x ₃ + … + a _{2 n} ⁽¹⁾ x_n = b ₂⁽¹⁾ ,

a ₃₂⁽¹⁾ x ₂ + a ₃₃⁽¹⁾ x ₃ + … + a _{3 n} ⁽¹⁾ x_n = b ₃⁽¹⁾,

...............

a_{n 2}⁽¹⁾ x ₂ + a_{n 3}⁽¹⁾ x ₃ + … + a_nn ⁽¹⁾ x_n = b_n ⁽¹⁾.

в которой a_ij ⁽¹⁾ и b_ij ⁽¹⁾ вычисляются по формулам

a_ij ⁽¹⁾ = a_ij − q_{i 1} a _{1 j}    , b_i ⁽¹⁾ = b_i − q_{i 1} b ₁.

2-й шаг. Целью этого шага является исключение неизвестного x ₂ из уравнений с номерами i = 3, 4, …, n. Пусть a ₂₂⁽¹⁾ ≠ 0, где a ₂₂⁽¹⁾ ­– коэффициент, называемый главным (или ведущим) элементом 2- го шага. Вычислим множители 2-го шага

q_{i 2} = a_{i 2}⁽¹⁾ / a ₂₂⁽¹⁾ (i = 3, 4, …, n)

и вычтем последовательно из третьего, четвертого, …, n-о го уравнения системы второе уравнение, умноженное соответственно на q ₃₂, q ₄₂, …, q_{m 2}. В результате получим систему

       a ₁₁ x ₁ + a ₁₂ x ₂ + a ₁₃ x ₃ + … + a _{1 n}x_n = b ₁ ,

                   a ₂₂⁽¹⁾ x ₂ + a ₂₃⁽¹⁾ x ₃ + … + a _{2 n} ⁽¹⁾ = b ₂⁽¹⁾ ,

                                   a ₃₃⁽²⁾ x ₃ + … + a _{3 n} ⁽²⁾ x_n = b ₃⁽²⁾ ,

...................

                                   a_{n 3}⁽²⁾ x ₃ + … + a_nn ⁽²⁾ x_n = b_n ⁽²⁾ .

Здесь коэффициенты a_ij ⁽²⁾ и b_ij ⁽²⁾ вычисляются по формулам

a_ij ⁽²⁾ = a_ij ⁽¹⁾ – q_{i 2} a _{2 j} ⁽¹⁾, b_i ⁽²⁾ = b_i ⁽¹⁾ – q_{i 2} b ₂⁽¹⁾.

Аналогично проводятся остальные шаги. Опишем очередной k- й шаг.

k- й шаг. В предположении, что главный (ведущий) элемент k-о го шага a_kk ^{( k –1)} отличен от нуля, вычислим множители k-го шага

q_ik = a_ik ^{(k –1)} / a_kk ^{(k –1)} (i = k + 1, …, n)

и вычтем последовательно из (k + 1)-го, …, n -го уравнений полученной на предыдущем шаге системы k -e уравнение, умноженное соответственно на q_{k +1, k}, q_{k +2, k}, …, q_nk.

После (n - 1)-го шага исключения получим систему уравнений

       a ₁₁ x ₁ + a ₁₂ x ₂ + a ₁₃ x ₃ + … + a _{1 n} x_n =   b ₁   ,

                   a ₂₂⁽¹⁾ x ₂ + a ₂₃⁽¹⁾ x ₃ + … + a _{2 n} ⁽¹⁾ x_n = b ₂⁽¹⁾ ,

                                   a ₃₃⁽²⁾ x ₃ + … + a _{3 n} ⁽²⁾ x_n = b ₃⁽²⁾ ,

      ....................

                                                           a_nn ^{(n –1)} x_n = b_n ^{(n –1)} .

матрица A ^{( n -1)} которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.