Обобщением простейшего потока является также поток с ограниченным последствием.
Рассмотрим ординарный поток однородных событий (рис.8)
| 0 |
| t |

|

|
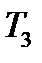
|
Рис.8
Этот поток называется потоком с ограниченным следствием (потоком Пальма) (Пальм, Конрад (1907—1951) — шведский инженер и ученый), если промежутки времени между последовательными событиями  представляют собой независимые случайные величины.
представляют собой независимые случайные величины.
Очевидно, простейший поток является частным случаем потока Пальма: в нём расстояния  представляют собой независимые случайные величины, которые распределены по экспоненциальному закону.
представляют собой независимые случайные величины, которые распределены по экспоненциальному закону.
Нестационарный пуассоновский поток не является потоком Пальма.
Рассмотрим пример потоков Пальма. Некоторая деталь технического устройства работает непрерывно до своего отказа, после чего она мгновенно заменяется новой. Срок безотказной работы детали является случайной величиной; отдельные экземпляры выходят из строя независимо один от другого. При этом условии поток отказов представляет собой поток Пальма. Если к тому же, срок работы детали распределен по экспоненциальному закону, то поток Пальма превращается в простейший поток.
Потоки Пальма часто получают в виде выходных потоков СМО. Если в любую систему поступает поток заявок, тогда он этой системой разделяется на два потока: поток обслуженных и поток не обслуженных заявок.
Поток не обслуженных заявок часто поступает в некоторую другую СМО, поэтому представляет интерес изучение его свойств.
Основной в теории выходных потоков являтся теорема Пальма: Пусть в СМО поступает поток заявок типа Пальма, причем заявка, которая застала все каналы занятыми, получает отказ (не обслуживается). Если при этом время обслуживания имеет экспоненциальный закон распределения, то поток заявок, которые не обслужены, является также потоком типа Пальма.
Поток Эрланга
Интересным примером потока с ограниченным последствием является так называемый поток Эрланга. Он образуется «просеиванием» простейшего потока.
Рассмотрим простейший поток (рис.9) и удалим из него каждую вторую точку (на рис.9 удаленные точки обозначены ромбами). Точки, которые остались, образуют поток; этот поток называется потоком Эрланга первого порядка ( ). Очевидно, этот поток является потоком Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то независимы и величины
). Очевидно, этот поток является потоком Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то независимы и величины  , которые получаются сложением таких промежутков по два.
, которые получаются сложением таких промежутков по два.
| 0 |
| t |
Рис.9
Поток Эрланга второго порядка( ) получим, если сохраним в простейшем потоке каждую третью точку, а две промежуточные удалим.
) получим, если сохраним в простейшем потоке каждую третью точку, а две промежуточные удалим.
| 0 |
| t |
Рис.10
Потоком Эрланга к-го порядка ( ) называется поток, получаемый из простейшего в случае сохранения каждой
) называется поток, получаемый из простейшего в случае сохранения каждой  -й точки, и удаления остальных точек. Очевидно, простейший поток можно рассматривать как поток Эрланга 0-го порядка (
-й точки, и удаления остальных точек. Очевидно, простейший поток можно рассматривать как поток Эрланга 0-го порядка (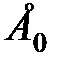 ).
).

|
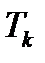
|

|
Рис.12
Закон распределения с плотностью
 ,(
,( ) (6.1)
) (6.1)
называется законом Эрланга к-го порядка.
Очевидно, при  он превращается в экспоненциальный закон
он превращается в экспоненциальный закон
 (
( ) (6.2)
) (6.2)
Характеристики закона Эрланга 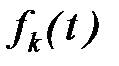 :
:
 (6.3)
(6.3)
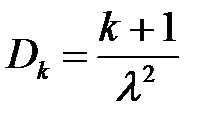 ,
,  (6.4)
(6.4)
Плотность  потока (
потока ( ) будет обратной величиной к математическому ожиданию
) будет обратной величиной к математическому ожиданию 
 (6.5)
(6.5)
Таким образом, при увеличении порядка потока Эрланга увеличивается как математическое ожидание, так и дисперсия промежутка времени между событиями, а плотность потока падает.
Пронормируем величину Т так, чтобы её математическое ожидание (а, значит, плотность потока) осталось неизменным. Для этого изменим масштаб по оси времени и вместо Т рассмотрим величину
 (6.6)
(6.6)
Назовем такой поток нормированным потоком Эрланга к-го порядка. Закон распределения промежутка  между событиями этого потока имеет вид
между событиями этого потока имеет вид
 (
( ) (6.7)
) (6.7)
где  или
или
 (
( ) (6.8)
) (6.8)
Математическое ожидание величины  , которая распределена по закону (6.8), не зависит от
, которая распределена по закону (6.8), не зависит от  и равно
и равно  , где
, где  – плотность потока, которая совпадает при любом
– плотность потока, которая совпадает при любом  с плотностью выходного простейшего потока. Дисперсия величины
с плотностью выходного простейшего потока. Дисперсия величины 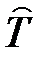 равна
равна
 (6.9)
(6.9)
и неограничено убывает с ростом  .
.
Таким образом, при неограниченном увеличении  нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными
нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными  .
.
Это свойство потока Эрланга является удобным в практическом применении. Оно даёт возможность, задавая разные значения  получать любую степень последействия: от полного отсутствия (
получать любую степень последействия: от полного отсутствия ( ) до жесткой функциональной зависимости между моментами появления события (
) до жесткой функциональной зависимости между моментами появления события ( ). С целью упрощения часто бывает удобным заменить реальный поток, имеющий последействие, нормированным потоком Эрланга с приблизительно теми же характеристиками промежутка между заявками: математическим ожиданием и дисперсией.
). С целью упрощения часто бывает удобным заменить реальный поток, имеющий последействие, нормированным потоком Эрланга с приблизительно теми же характеристиками промежутка между заявками: математическим ожиданием и дисперсией.
Пример. В результате статистической обработки промежутков между заявками в потоке получены оценки для математического ожидания и дисперсии величины Т: 
 .
.
Решение. Имеем 
Из формулы (5.11) получим 
 . Поток можно приближенно заменить нормированным потоком Эрланга четвертого порядка.
. Поток можно приближенно заменить нормированным потоком Эрланга четвертого порядка.
Время обслуживания
Кроме характеристик входного потока заявок, режим работы системы зависит еще от характеристик продуктивности самой системы: числа каналов  и быстродействия каждого канала. Одной из важнейших величин, связанных с системой, является время обслуживания одной заявки
и быстродействия каждого канала. Одной из важнейших величин, связанных с системой, является время обслуживания одной заявки  . Эта величина может быть как неслучайной, так и случайной.
. Эта величина может быть как неслучайной, так и случайной.
Рассмотрим случайную величину  и обозначим
и обозначим  её функцию распределения:
её функцию распределения:
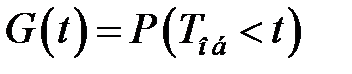 (6.1)
(6.1)
а  – плотность распределения:
– плотность распределения:
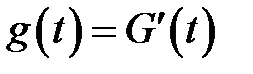 (6.2)
(6.2)
Для практики особенный интерес имеет случай, когда величина  распределена по экспоненциальному закону
распределена по экспоненциальному закону
 (
( ), (6.3)
), (6.3)
где параметр  – величина, обратная к среднему времени обслуживания одной заявки:
– величина, обратная к среднему времени обслуживания одной заявки:
 , (6.4)
, (6.4)
Особая роль, которую играет в теории МО экспоненциальный закон распределения  , связана с его свойством отсутствия последствия. В применении к данному случаю: если в некоторый момент
, связана с его свойством отсутствия последствия. В применении к данному случаю: если в некоторый момент 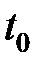 происходит обслуживание заявки, то закон распределения времени, которое осталось до конца обслуживания, не зависит от того времени сколько обслуживание уже продолжалось.
происходит обслуживание заявки, то закон распределения времени, которое осталось до конца обслуживания, не зависит от того времени сколько обслуживание уже продолжалось.
Понятно, что экспоненциальный закон не является универсальным законом распределения времени обслуживания. Часто время обслуживания лучше описывается, например, законом Эрланга. Однако, пропускная способность и другие характеристики СМО сравнительно мало зависят от времени обслуживания, а зависят, главным образом, от его среднего значения  . Поэтому в теории МО чаще всего пользуются допущением, что время обслуживания распределено по экспоненциальному закону. Эта гипотеза позволяет существенно упростить математический аппарат, который применяется для решения задач МО, и, в ряде случаев, получить простые аналитические формулы для характеристики пропускной способност системы.
. Поэтому в теории МО чаще всего пользуются допущением, что время обслуживания распределено по экспоненциальному закону. Эта гипотеза позволяет существенно упростить математический аппарат, который применяется для решения задач МО, и, в ряде случаев, получить простые аналитические формулы для характеристики пропускной способност системы.
 2020-05-12
2020-05-12 467
467








