Допущения о пуассоновском характере потока заявок и об экспоненциальном распределении времени обслуживания позволяют применять в теории МО аппарат так называемых марковских случайных процессов.
Процесс, протекающий в физической системе, называется марковским или процессом без последействия, если для каждого момента времени вероятность любого состояния системы в будущем зависит лишь от состояния системы в данный момент (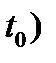 и не зависит от того, каким образом система попала в это состояние.
и не зависит от того, каким образом система попала в это состояние.
Рассмотрим пример. Пусть дано техническое устройство Х, состоящее из элементов (деталей) типа  и
и  , которые имеют разную долговечность. Эти элементы в случайные моменты времени и независимо один от другого могут выходить из строя. Слаженная работа каждого элемента, безусловно, необходима для работы устройства в целом. Время безотказной работы элемента – случайная величина, распределенная по экспоненциальному закону с соответствующими параметрами
, которые имеют разную долговечность. Эти элементы в случайные моменты времени и независимо один от другого могут выходить из строя. Слаженная работа каждого элемента, безусловно, необходима для работы устройства в целом. Время безотказной работы элемента – случайная величина, распределенная по экспоненциальному закону с соответствующими параметрами 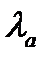 и
и  . В случае отказа устройства мгновенно принимаются меры для выявления причин, и выявленный неисправный элемент в то же время заменяется новым. Время, необходимое для ремонта устройства, распределено по экспоненциальному закону с параметром
. В случае отказа устройства мгновенно принимаются меры для выявления причин, и выявленный неисправный элемент в то же время заменяется новым. Время, необходимое для ремонта устройства, распределено по экспоненциальному закону с параметром 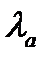 или
или  соответственно. В этом примере случайный процесс, протекающий в системе, является марковским процессом с непрерывным временем и конечным множеством состояний:
соответственно. В этом примере случайный процесс, протекающий в системе, является марковским процессом с непрерывным временем и конечным множеством состояний: 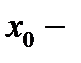 все элементы исправные, система работает;
все элементы исправные, система работает;  неисправный элемент типа
неисправный элемент типа 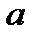 , система ремонтируется;
, система ремонтируется;  неисправный элемент типа
неисправный элемент типа  , система ремонтируется. Схема возможных переходов показана на рис.13.
, система ремонтируется. Схема возможных переходов показана на рис.13.
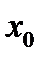
|

|

|
Рис.13.
В случае, когда процесс, протекающий в физической системе с конечным множеством состояний и непрерывным временем, является марковским, можно описать за помощью обыкновенных дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний 
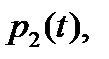 …
…
 2020-05-12
2020-05-12 124
124







