Простейший поток событий

Потоком событий называется последовательность событий, которые наступают одно за другим в отдельные моменты времени.

Таким потоком будет, например, поток вызовов в сфере обслуживания (ремонт телевизоров, заказы в ателье, химчистке и т.д.), вызовы на станции скорой помощи, телефонной станции, очередь на заправке и т.п.

Поток называется простейшим, если выполняются следующие условия:

1) вероятность наступления события пропорциональна длине промежутка времени ;

2) вероятность появления события на любом промежутке времени не зависит от того, какое число событий наступило до этого промежутка;

3) вероятность одновременного наступления двух или более событий считается пренебрежимо малой.

Пусть известно среднее число наступлений события  в единицу времени . Определим вероятность того, что за промежуток времени 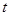 событие  наступит  раз.

Разделим промежуток времени на 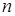 частей, 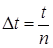. Вероятность, что в течение  событие наступит, равна 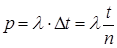, обратная вероятность, что событие не наступит, равна . Тогда вероятность того, что за все время 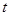 событие произойдет  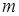раз, можно подсчитать как вероятность того, что на  промежутках оно наступит, а на  не наступит:

                                .

Для определения истинного значения вероятности нужно найти предел:

                           .

Используя преобразования, аналогичные тем, что применялись в пункте 30.3. получим

                                       .

Полученная формула носит название формулы Пуассона. Поток событий, к которому она применима, также называется пуассоновским.

Пример. На станцию скорой помощи поступает в среднем 90 вызовов в час. Какова вероятность, что за 4 минуты произойдет а) один вызов;б) хотя бы один вызов?

а) Нужную вероятность вычислим по формуле Пуассона, используя среднее число вызовов в минуту : .

б) Искомую вероятность найдем, используя вероятность обратного события, что не произойдет ни одного вызова:

           .