Числовые характеристики ДСВ

Числовые характеристики служат для краткого описания ДСВ и делятся на две группы: характеристики положения и характеристики разброса. К первым относятся математическое ожидание, мода и медиана случайной величины. Дадим их определения:

1) Математическим ожиданием  дискретной случайной величины  называется значение, определяемое следующей формулой:

                       .

Математическое ожидание представляет собой средневзвешенное всех значений Х (“весами” служат вероятности отдельных значений) и характеризует порядок величины (десятые, сотые, целые числа, десятки, сотни и т. д.).

                                      .

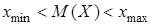Для разобранного в данном разделе примера

                 .

2) Модой  случайной величины называется ее значение, имеющее наибольшую вероятность. В нашем примере = 2.

3) Медианой случайной величины называется такое ее значение, для которого выполняется следующее условие:

                                        

Медиана — такое значение случайной величины, для которого функция распределения равна 0. 5.

Рассмотрим теперь характеристики разброса. Необходимость их введения можно пояснить на примере.

Пусть заданы две случайные величины  и .

	8	9	10	11	12
	0,2	0,2	0,2	0,2	0,2
	– 10	0	10	20	30
	0,2	0,2	0,2	0,2	0,2

По данным из таблицы найдем математическое ожидание

,

.

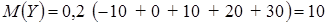Видно, что при одной и той же величине математического ожидания, отдельные значения  отличаются от  гораздо меньше, чем отдельные значения  от . Числовые характеристики, определения которых сейчас будут даны, учитывают эту разницу в поведении случайных величин.

1) Дисперсией  случайной величины Х называется математическое ожидание квадрата отклонения Х от своего математического ожидания. Для ДСВ дисперсия вычисляется по формуле:

                                .

Преобразование этой формулы позволяет привести ее к более удобному виду:

Используя аналогию с  можно обозначить .

Тогда .

Дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания.

Вычислим значение дисперсии для случайной величины Х, рассмотренной в примере. По первой формуле:

.

По второй формуле:

.

Следует помнить, что, по своему определению, дисперсия — величина неотрицательная, т. е. .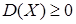

2) Среднеквадратическим отклонением 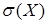 случайной величины Х называется корень квадратный из дисперсии:

                                         .

Характеристика вводится, чтобы иметь возможность указать разброс в той же размерности, что и сама случайная величина (т. к. дисперсия имеет размерность квадрата Х).

Для нашего примера 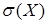= 0. 81.

Среднеквадратическое отклонение имеет смысл абсолютной погрешности при замене Х ее математическим ожиданием.

3) Вариацией  случайной величины Х называется отношение .

Вариация имеет смысл относительной погрешности.

 31.4. Способы представления непрерывной случайной величины  

Пусть непрерывная случайная величина Х принимает значения из некоторого промежутка . Значения  и , в зависимости от конкретных условий, могут быть различными, а сам промежуток   может быть конечным (например, [–1,2]), полубесконечным (например, (- ,0] или [3, )) или бесконечным . Подразумевается, что . Все значения, попадающие на 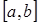, невозможно перечислить, поэтому невозможно и указать, какие вероятности им соответствуют. Чтобы охарактеризовать распределение вероятностей в этом случае, поступают так. На  выделяют участок от  до  и находят отношение вероятности попадания на этот участок  к длине участка:

                                           .

 представляет собой среднюю вероятность, приходящуюся на единицу измерения Х, вычисленную на участке . По аналогии с плотностью (массой, приходящейся на единицу объема) она может быть названа средней плотностью вероятности. Средняя плотность вероятности зависит и от положения точки , и от длины участка . Чтобы исключить влияние , его стараются взять как можно меньшим, т. е. находят предел:

.

Функция  называется плотностью вероятности (или плотностью распределения вероятности). Она должна удовлетворять следующему требованию:

 .

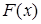Как и для ДСВ, вводится понятие функции распределения: . Между функциями  и  имеется тесная связь:

;

.

Т. е. плотность вероятности  является производной от функции распределения 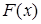 и, наоборот, функция распределения  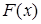является первообразной для плотности вероятности, ее можно найти по формуле:

.

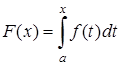 В связи с этим,  называют иногда дифференциальной функцией распределения, а 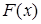 — интегральной. Свойства функции 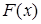для НСВ аналогичны свойствам функции распределения для ДСВ.

С помощью функции распределения можно найти вероятность попадания значений случайной величины  на промежуток :

.