2020-05-12
482
В аналитической геометрии на плоскости одна из основных задач состоит в приведении общего уравнения линии второго порядка к каноническому виду путём перехода к соответствующей системе координат. Теория квадратичных форм имеет своей целью решение аналогичных задач в пространстве любого числа измерений.
Определение. Числовая функция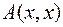 
одного векторного аргумента 
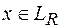, полученная из симметричной билинейной формы 
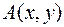заменой 
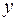на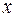 
, называется квадратичной формой.
Например, скалярный квадрат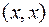 
есть квадратичная форма.
Симметричная билинейная форма 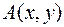называется полярной к квадратичной форме .
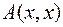В вещественном евклидовом пространстве скалярное произведение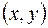 
есть билинейная форма, полярная положительно определённой квадратичной форме 
.
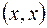В вещественном линейном пространстве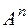 
с фиксированным базисом 
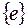квадратичная форма имеет вид
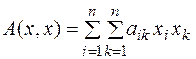, (1)
где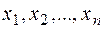 
- координаты вектора 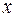в базисе , 
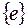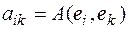- значения формы на базисных векторах. Числа 
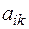образуют матрицу 
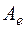квадратичной формы в базисе : 
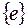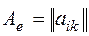, эта матрица симметрична, т.е. 
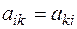. При изменении базиса 
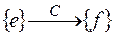матрица квадратичной формы изменяется так же, как матрица соответствующей симметричной билинейной формы, т.е. по закону
. 
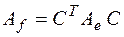Значит, ранг матрицы квадратичной формы не зависит от выбора базиса. Поэтому можно ввести понятие ранга квадратичной формы как ранга ее матрицы в любом базисе. Квадратичная форма, ранг которой совпадает с размерностью пространства, называется невырожденной.
В дальнейшем будем использовать следующую терминологию.
Квадратичная форма 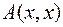называется
1) положительно (отрицательно) определённой, если для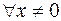 
выполняется неравенство
,
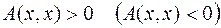при этом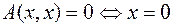 
(такие формы называются знакоопределёнными);
2) знакопеременной, если существуют такие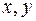 
, что
;
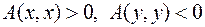3) квазизнакоопределённой, если для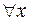 
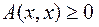или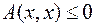 
,
но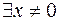 
, для которого 
.
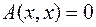Примеры. 1) Рассмотрим в пространстве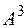 
квадратичную форму 
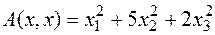. Очевидно, она является положительно определённой.
2) Квадратичная форма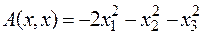 
отрицательно определена.
3) Квадратичная форма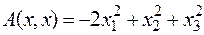 
знакопеременна. Действительно, 
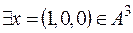, для которого 
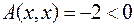, и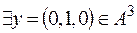 
, для которого 
.
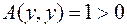4) Квадратичная форма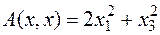 
является квазиположительно определённой: 
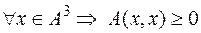, но существует ненулевой вектор 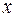, например, 
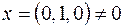, для которого .
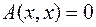В дальнейшем будут сформулированы признаки, по которым можно судить о принадлежности квадратичной формы к одному из указанных типов. Укажем также методы выбора такого базиса 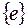, в котором матрица квадратичной формы имеет диагональный вид
,
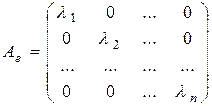т.е. сама форма приводится к сумме квадратов
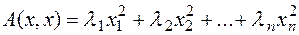. (2)
Выражение (2) называется каноническим видом квадратичной формы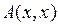 
, коэффициенты 
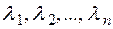- каноническими коэффициентами. Базис, в котором квадратичная форма имеет вид (2), называется каноническим.
Так как ранг квадратичной формы инвариантен относительно изменения базиса, то он равен количеству отличных от нуля канонических коэффициентов. Оставляя в представлении (2) лишь отличные от нуля коэффициенты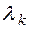 
и при необходимости перенумеровывая их, получим 
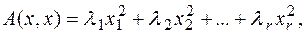где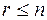 
- ранг квадратичной формы, называемый также её индексом инерции.
