Метод Якоби.
Метод Якоби позволяет не только указать явные формулы перехода от заданного базиса к каноническому, но и получить формулы для канонических коэффициентов  . Однако для этого квадратичная форма
. Однако для этого квадратичная форма  должна удовлетворять некоторым условиям.
должна удовлетворять некоторым условиям.
Теорема (Якоби). Пусть в базисе 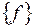 квадратичная форма (1) имеет вид
квадратичная форма (1) имеет вид
 где
где 
И пусть определители (угловые миноры матрицы квадратичной формы)

отличны от нуля. Тогда существует канонический базис  , в котором квадратичная форма
, в котором квадратичная форма  записывается в виде суммы квадратов:
записывается в виде суммы квадратов:
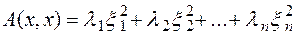 .
.
Здесь  - координаты вектора
- координаты вектора  в базисе
в базисе  , а канонические коэффициенты
, а канонические коэффициенты 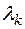 определяются формулами
определяются формулами
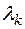 =
=  ,
, 

Доказательство. Наша цель – определить базисные векторы 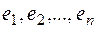 так, чтобы элементы матрицы
так, чтобы элементы матрицы  , расположенные вне главной диагонали, равнялись нулю
, расположенные вне главной диагонали, равнялись нулю
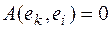 при
при 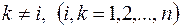 , (7)
, (7)
 . (8)
. (8)
Процесс, с помощью которого это будет сделано, аналогичен процессу ортогонализации (п. 32). Будем искать векторы канонического базиса  в виде
в виде
 (9)
(9)
Таким образом, задача сводится к определению коэффициентов  . Эти коэффициенты можно было бы найти из условий (7), подставляя в них вместо каждого аргумента
. Эти коэффициенты можно было бы найти из условий (7), подставляя в них вместо каждого аргумента  соответствующие выражения из (9):
соответствующие выражения из (9):

Но в таком случае приходим к системе уравнений второй степени относительно неизвестных  . Чтобы получить линейную систему (которую мы уже умеем решать), заметим сначала, что для
. Чтобы получить линейную систему (которую мы уже умеем решать), заметим сначала, что для  из соотношений
из соотношений  вытекает, что и
вытекает, что и  . Действительно, разворачивая в выражении
. Действительно, разворачивая в выражении 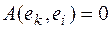 только второй аргумент
только второй аргумент  , получим
, получим

Отсюда следует, что если  для
для  и
и 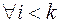 , то и
, то и  для
для 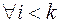 . А в силу симметрии матрицы квадратичной формы
. А в силу симметрии матрицы квадратичной формы 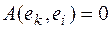 и для
и для  .
.
С учетом изложенного задача сводится к следующему: определить коэффициенты  так, чтобы базисный вектор
так, чтобы базисный вектор

удовлетворял условиям
 . (10)
. (10)
К этим условиям, определяющим вектор 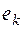 с точностью до постоянного множителя, добавим условие
с точностью до постоянного множителя, добавим условие
 . (11)
. (11)
Всего записано 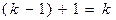 условий для определения
условий для определения  неизвестных коэффициентов
неизвестных коэффициентов  .
.
Положим в (10)  и развернем аргумент
и развернем аргумент 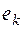 :
:
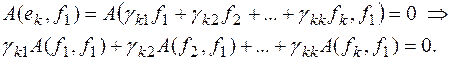
Вспоминая, что 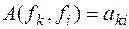 - элементы заданной симметричной матрицы, запишем результат в виде
- элементы заданной симметричной матрицы, запишем результат в виде 
Полагая в (10)  , получим еще (
, получим еще ( ) линейных однородных уравнений относительно
) линейных однородных уравнений относительно  . Наконец, из (11) получаем последнее (уже неоднородное) уравнение.
. Наконец, из (11) получаем последнее (уже неоднородное) уравнение.
В результате приходим к линейной системе
 (12)
(12)
относительно  неизвестных
неизвестных  . Определитель этой системы
. Определитель этой системы

по условию отличен от нуля для  . Поэтому система (12) – крамеровская, значит, совместна и определена, её единственное решение
. Поэтому система (12) – крамеровская, значит, совместна и определена, её единственное решение  всегда можно найти. Таким образом, задача определения любого вектора
всегда можно найти. Таким образом, задача определения любого вектора 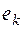 канонического базиса решена.
канонического базиса решена.
Остаётся найти канонические коэффициенты  (коэффициенты формы
(коэффициенты формы  в каноническом базисе
в каноническом базисе  ). По условию (8)
). По условию (8)  . Вычислим
. Вычислим 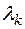 , разворачивая в
, разворачивая в  только второй аргумент:
только второй аргумент:




Но в силу условий (10) здесь отлично от нуля только последнее слагаемое, равное 1 в силу (11), т.е. остаётся  . Из системы (12) по формуле Крамера находим
. Из системы (12) по формуле Крамера находим  :
:
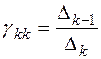 =
=  .¨ (13)
.¨ (13)
Замечание 1. Исходные базисные векторы  можно было занумеровать в другом порядке, не говоря уж о том, что базис
можно было занумеровать в другом порядке, не говоря уж о том, что базис  не обязательно было искать в виде (5). Это еще раз свидетельствует о том, что канонический базис не определяется единственным образом.
не обязательно было искать в виде (5). Это еще раз свидетельствует о том, что канонический базис не определяется единственным образом.
Пример. Рассмотрим квадратичную форму
 .
.
в пространстве  с базисом
с базисом 
Напоминаем, что матрица квадратичной формы симметрична, т.е.


 .
.
Аналогично 
 . Наконец,
. Наконец,  . Поэтому матрица формы в заданном базисе
. Поэтому матрица формы в заданном базисе  имеет вид
имеет вид
 .
.
Вычислим миноры: 
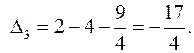
Все они отличны от нуля - условия теоремы Якоби выполнены. Ищем векторы канонического базиса  в виде
в виде
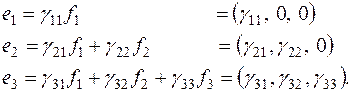
Для облегчения последующих вычислений запишем симметричную билинейную форму, соответствующую заданной квадратичной форме:
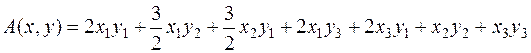 .
.
Коэффициент  находим из условия
находим из условия 
Значит,  .
.
Чтобы записать вектор  , надо найти коэффициенты
, надо найти коэффициенты  и
и  . Для их определения имеем два условия:
. Для их определения имеем два условия:
 и
и  .
.
Решаем систему 
Значит,  .
.
Наконец, для вектора  (т.е. для коэффициентов
(т.е. для коэффициентов  ,
,  и
и  ) имеем три условия:
) имеем три условия:
 и
и  .
.
Решаем систему

Значит,  .
.
Остаётся вычислить канонические коэффициенты по формулам (13)

и записать вид квадратичной формы в каноническом базисе  :
:
 .¨
.¨
Замечание 2. В теореме доказано, что при условии 
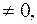
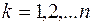 квадратичная форма приводится к каноническому виду
квадратичная форма приводится к каноническому виду
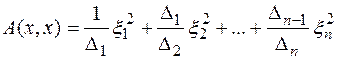 .
.
Можно ослабить условия, потребовав 
 , т.е.
, т.е. 
 (допускается, что
(допускается, что  может равняться нулю), и доказать, что форма может быть приведена к каноническому виду
может равняться нулю), и доказать, что форма может быть приведена к каноническому виду
 .
.
 2020-05-12
2020-05-12 3254
3254