Приведение квадратичной формы к каноническому виду

Метод Лагранжа

 

       Напомним, что каждому преобразованию базиса соответствует невырожденное линейное преобразование координат, и наоборот. Поэтому вопрос о приведении квадратичной формы к каноническому виду можно решить с помощью соответствующего преобразования координат.

       Теорема (Лагранж). Любая квадратичная форма 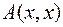, заданная в -мерном пространстве, с помощью невырожденного линейного преобразования координат может быть приведена к каноническому виду (2).

       Доказательство. В основе доказательства лежит идея дополнения квадратного трёхчлена до полного квадрата.

1) Сначала предположим, что в квадратичной форме (1) имеется хотя бы один диагональный коэффициент . Не ограничивая общности, можем всегда считать, что  (добиться этого можно, перенумеровав переменные, т.е. произведя невырожденное преобразование координат). Выделим в выражении (1) все слагаемые, содержащие координату :

.  (3)

 

Выделенную группу преобразуем, дополняя до полного квадрата:

.

 

Здесь использовано правило возведения в квадрат суммы нескольких слагаемых:

.

Подключим не вошедшие в скобки слагаемые (квадраты координат  и удвоенные произведения всевозможных пар координат, кроме ) к двойной сумме. Квадратичная форма (3) принимает вид

,                  (4)

где коэффициенты , если , и , если . Обращаем внимание на то, что двойная сумма уже не содержит координаты .

 

       Назовём выражение в круглых скобках новой координатой , а координаты  переобозначим  соответственно. Получим невырожденное преобразование координат

,

 

 

Действительно, определитель

.

С помощью этого преобразования и представления (4) форма 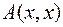 принимает вид

,

где квадратичная форма  не содержит координаты .

       2) Пусть в квадратичной форме (1) все диагональные коэффициенты равны нулю, но тогда  (ведь форма 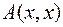 не равна тождественно нулю). Будем считать, например, что . В этом случае поможет следующее невырожденное (проверьте!) преобразование координат (для удобства выразим старые координаты через новые):

.

В результате слагаемое  преобразуется следующим образом:

= .

И в форме 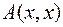 появляются сразу два квадрата координат с отличными от нуля коэффициентами. Таким образом, задача сводится к предыдущей.

 

       Последовательным комбинированием приёмов 1) и 2) можно за конечное число шагов привести любую квадратичную форму к сумме квадратов - в этом безусловное преимущество метода Лагранжа. Однако этот метод не дает возможности непосредственного вычисления (по заданной матрице) ни канонических коэффициентов 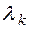, ни координат векторов канонического базиса.

 

       Пример. Приведём методом Лагранжа к каноническому виду квадратичную форму, определённую в пространстве :

.

1-ый шаг. Выделяем группу слагаемых с координатой  и дополняем до полного квадрата:

 

Выражение в круглых скобках подсказывает преобразование координат:

 с матрицей .

Теперь выделенная группа принимает вид

,

а для всей формы получаем

.

2-й шаг. Выделяем группу слагаемых с координатой  и дополняем до полного квадрата:

.

Запишем соответствующее преобразование координат:

 с матрицей ..

Выделенная группа принимает вид

,

а для всей формы получаем

.

3-ий шаг. В последнем результате отсутствуют квадраты координат  и . Поэтому полагаем

 с матрицей

Теперь . Координаты  и  переобозначены соответственно через  и . Таким образом, форма приведена к каноническому виду

.                                           (5)

Поскольку отличны от нуля все четыре канонических коэффициента, то ранг  данной формы совпадает с размерностью  пространства - форма невырожденная.

Перемножим три последовательных невырожденных преобразования

=

Значит, невырожденное преобразование с матрицей  переводит старые координаты в новые

 

Это преобразование приводит квадратичную форму к каноническому виду (5).

 

Предлагаем самостоятельно выписать преобразование базиса, соответствующее каждому из произведенных преобразований координат. Напоминаем, что матрица, с помощью которой векторы нового базиса выражаются через векторы старого базиса, и матрица, выражающая новые координаты через старые, являются взаимно обратными (см. 35. Переход к новому базису. Преобразование координат).

 

В каноническом виде (5) можно сделать ещё одно преобразование координат - нормировку:

,

в результате квадратичная форма приводится к нормальному виду

                                                       (6)

с каноническими коэффициентами, равными +1 или -1.¨

 

       Замечание. Поскольку 1-ый шаг мы могли проделать с любой из четырёх координат (а не обязательно с ), то ясно, что ни канонический вид, ни канонический базис квадратичной формы не определяются однозначно.