2020-05-11
1808
В алгебраическую
Перевод комплексных чисел из показательной формы записи в алгебраическую, осуществляются по формуле Эйлера через тригонометрическую форму записи. Рассмотрим этот перевод на примере комплексного сопротивления.
а) Z = z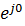 
= z cos 
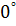+ j z sin 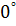= R.
Действительная часть комплексного сопротивления равна активному сопротивлению R, на схеме такая цепь изображается:
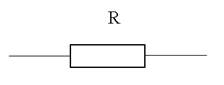
б) Z = z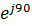 
= z cos 
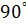+ j z sin 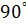= j z = j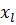 
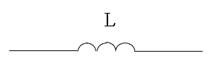
Коэффициент при «+j» равен индуктивному сопротивлению цепи 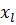, на схеме такая цепь изображается:
в) Z = z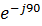 
= z cos 
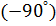+ j z sin 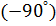= – j z = – j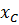 
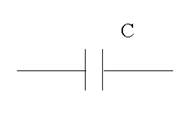
Коэффициент при «–j» равен емкостному сопротивлению цепи 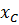, на схеме такая цепь изображается:
г) Z = z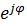 
= z cos 
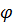+ j z sin 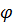= R + j 
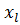. На схеме такая цепь изображается:
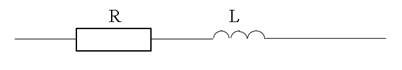
д) Z = z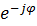 
= z cos 
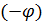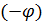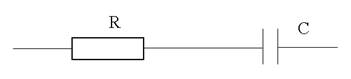
+ j z sin = R -j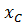 
. На схеме такая цепь изображается:
Перевод комплексного числа алгебраической формы в показательную. Действия с комплексными числами
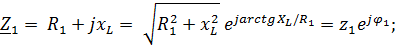
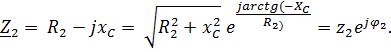
Деление и умножение комплексных чисел можно производить:
а) В алгебраической форме. При делении в алгебраической форме числитель и знаменатель дроби домножаются на комплексное число, сопряженное знаменателю (комплексное число, у которого перед «j» меняется знак на противоположный).
Произведение двух комплексно-сопряженных чисел равно сумме квадратов действительной и мнимой части (коэффициента при «j») исходного числа.
При умножении комплексных чисел произведение:
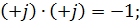
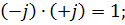
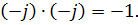
б) В показательной форме. При перемножении комплексных чисел в показательной форме показатели степени при «j» складываются алгебраически, при делении показатель степени при «j» знаменателя вычитается из показателя степени при «j» числителя.
