Как было сказано выше, расчет цепей синусоидального тока в комплексном виде можно производить всеми известными методами расчета цепей постоянного тока: методом эквивалентных преобразований, применением законов Кирхгофа, методом узловых потенциалов, методом контурных токов и т.п.
Расчет цепей с одним источником энергии проще производить методом эквивалентных преобразований. Этот метод заключается в том, что, преобразуя схему, приводим ее к схеме с последовательным соединением сопротивлений.
Пример такого преобразования см. в пункте 2.6, пример 2.1.
Расчет цепи методом эквивалентных преобразований производится с помощью закона Ома:

где 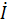 – комплексное действующее значение тока;
– комплексное действующее значение тока; 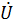 – комплексное действующее значение напряжения; Z – комплексное сопротивление цепи.
– комплексное действующее значение напряжения; Z – комплексное сопротивление цепи.
Z = R + j  - j
- j 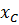 = R + j(
= R + j(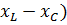 = z
= z 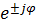 ,
,
где R – активное сопротивление цепи, Ом; j  – комплексное индуктивное сопротивление цепи;
– комплексное индуктивное сопротивление цепи;  =
= 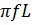 =
=  – модуль (величина) индуктивного сопротивления цепи, Ом; – j
– модуль (величина) индуктивного сопротивления цепи, Ом; – j 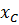 – комплексное емкостное сопротивление цепи;
– комплексное емкостное сопротивление цепи; 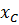 = 1/2(
= 1/2( ) = 1/(
) = 1/(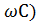 – модуль емкостного сопротивления цепи, Ом; j(
– модуль емкостного сопротивления цепи, Ом; j(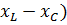 – комплексное реактивное сопротивление цепи; (
– комплексное реактивное сопротивление цепи; (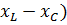 – модуль реактивного сопротивления цепи, Ом; z =
– модуль реактивного сопротивления цепи, Ом; z = 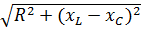 – модуль полного комплексного сопротивления цепи, Ом.
– модуль полного комплексного сопротивления цепи, Ом.
Угол 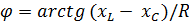 в зависимости от величин R,
в зависимости от величин R, 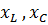 цепи может принимать различные значения 0 до
цепи может принимать различные значения 0 до 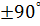 .
.
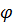 = 0 – при идеальном активном сопротивлении цепи (Z = R);
= 0 – при идеальном активном сопротивлении цепи (Z = R);
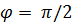 – при идеальном индуктивном сопротивлении цепи (Z =
– при идеальном индуктивном сопротивлении цепи (Z = 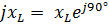 );
);
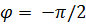 – при идеальном емкостном сопротивлении цепи (Z =
– при идеальном емкостном сопротивлении цепи (Z = 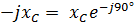 );
);
0 < 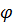 <
< 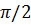 – при активно-индуктивном сопротивлении цепи (Z =
– при активно-индуктивном сопротивлении цепи (Z =  );
);
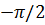 <
< 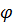 < 0 – при активно-емкостном сопротивлении цепи (Z =
< 0 – при активно-емкостном сопротивлении цепи (Z =  ).
).
Сопротивления цепи могут быть соединены:
1. Последовательно (рис. 2.2.): по всем элементам цепи протекает один и тот же ток 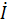 =
= 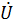 / Z.
/ Z.
Сопротивление цепи:
Z = 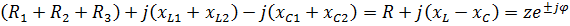 , Ом,
, Ом,
где R = 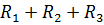 , Ом;
, Ом;  =
= 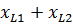 , Ом;
, Ом; 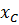 =
=  , Ом; z =
, Ом; z = 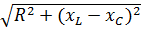 , Ом;
, Ом; 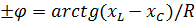 , «
, «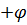 », если
», если 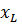 >
> 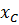 ; «
; «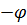 », если
», если 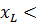
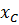 .
.

Рис. 2.2
2. Параллельно (рис. 2.3): по каждой ветви цепи протекает свой ток 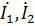 , а в неразветвленной цепи – ток
, а в неразветвленной цепи – ток 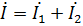 .
.

Рис. 2.3
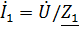 ,
,  ,
,
где 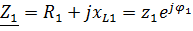 ,
, 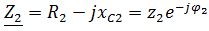 ,
,
 .
.
3. Смешанное соединение (рис. 2.4):
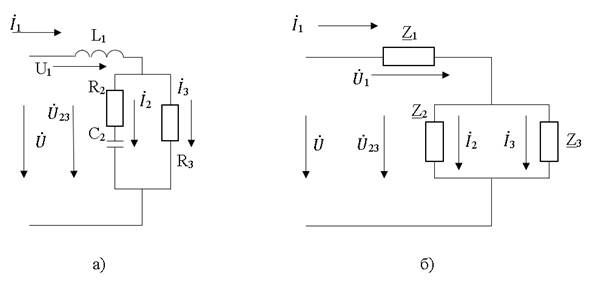
Рис. 2.4
Например, 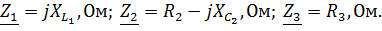
Для расчета такой цепи находится общее сопротивление Z. Сопротивления 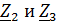 соединены параллельно
соединены параллельно 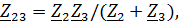 Ом.
Ом.
Сопротивление 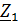 оказывается при этом соединенным последовательно с
оказывается при этом соединенным последовательно с 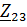 Z =
Z = 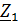 +
+ 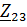 , Ом. Схема рис. 2.4. превращается в схему рис. 2.5.
, Ом. Схема рис. 2.4. превращается в схему рис. 2.5.
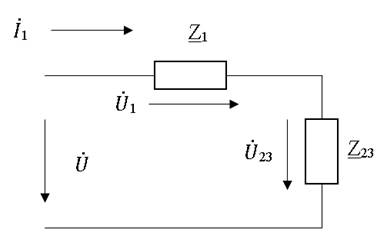
Рис. 2.5
Ток 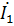 определяется по закону Ома:
определяется по закону Ома: 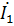 =
= 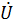 / Z.
/ Z.
Для определения токов 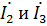 воспользуемся законом Ома для участка цепи. Определим напряжение на параллельном участке цепи
воспользуемся законом Ома для участка цепи. Определим напряжение на параллельном участке цепи  :
:
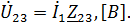
После чего найдем искомые токи в ветвях: 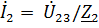 , [A];
, [A]; 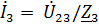 , [A];
, [A];
После нахождения всех токов необходимо выполнить проверку, чтобы убедиться в правильности расчета:
- по первому закону Кирхгофа: 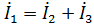 ;
;
- по второму закону Кирхгофа: 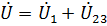 , где
, где 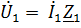 .
.
Баланс мощности
На основании закона сохранения энергии, суммарная мощность источников энергии должна быть равна суммарной мощности приемников:
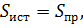
где 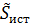 =
= 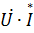 =
= 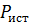 ± j
± j 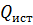 =
= 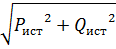
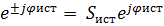 ;
;
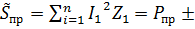 j
j  ;
;
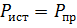 ;
; 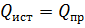 ;
; 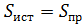 .
.
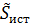 – комплексная мощность источника энергии;
– комплексная мощность источника энергии; 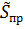 – комплексная мощность источника энергии;
– комплексная мощность источника энергии; 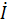 – комплексный ток, А;
– комплексный ток, А; 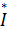 – сопряженный комплекс тока
– сопряженный комплекс тока 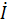 , A,
, A, 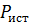 – активная мощность источника цепи, Вт;
– активная мощность источника цепи, Вт; 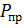 – активная мощность приемников цепи, Вт;
– активная мощность приемников цепи, Вт; 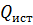 – реактивная мощность источников цепи, вар;
– реактивная мощность источников цепи, вар;  – реактивная мощность приемников цепи, вар.
– реактивная мощность приемников цепи, вар. 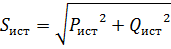 – полная мощность источников цепи, ВА;
– полная мощность источников цепи, ВА; 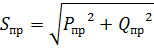 – полная мощность приемников цепи, ВА.
– полная мощность приемников цепи, ВА.
Баланс мощности является также проверкой правильности расчета цепи.
Векторная диаграмма строится на комплексной плоскости и представляет совокупность векторов токов и напряжений цепи.
Векторная диаграмма позволяет проверить правильность расчетов цепи.
Построение векторной диаграммы надо начинать с выбора масштаба напряжений и токов. Векторная диаграмма может быть построена как в показательной, так и в алгебраической форме записи комплексных величин.
При построении векторной диаграммы в показательной форме надо иметь в виду, что:
- За условно положительное направление вращения в электротехнике принято направление против часовой стрелки, поэтому начальные фазы векторов откладываются от оси +1 против часовой стрелки, если они положительны и по часовой стрелке, если отрицательны.
- Направление угла 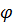 показывается от тока к напряжению.
показывается от тока к напряжению.
При построении векторной диаграммы в алгебраической форме по действительной оси откладывается действительная часть комплексного числа, а по мнимой – коэффициент при «j» в выбранном масштабе.
Рассмотрим пример построения векторной диаграммы (при записи расчетных значений в показательной – рис. 2.6 и алгебраической – рис. 2.7 формах) для следующих данных:
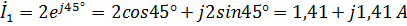 ;
;
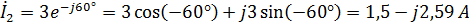 ;
;
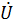 = 220
= 220 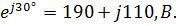
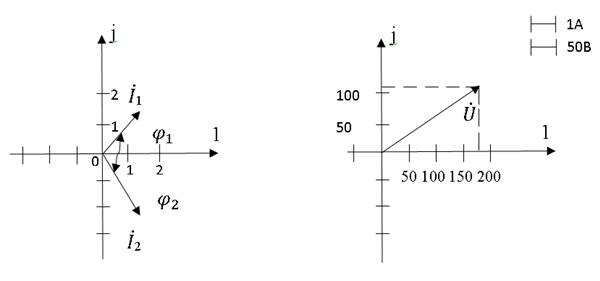
Рис. 2.6 Рис. 2.7
На векторной диаграмме можно производить сложение и вычитание векторов.
При построении векторной диаграммы в домашнем задании, диаграммы токов и напряжений строятся на одном чертеже (см. рис. 2.10), при этом каждая из них строятся в своем масштабе!
Примеры расчета
1. Исходная схема цепи приведена на рис. 2.1.
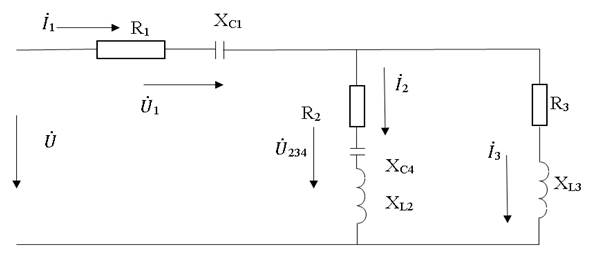
Рис. 2.8.
2. Исходные данные для составления расчетной схемы и дальнейших расчетов (табл. 2.1):
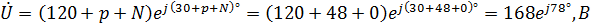 .
.
Z 1= 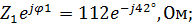 Z 2=
Z 2= 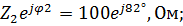
Z 3= 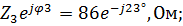 Z 4=
Z 4= 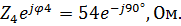
3. Для составления расчетной схемы и определения параметров цепи переведем комплексные сопротивления Z 1, Z 2, Z 3, Z 4, записанные в показательной форме, в алгебраическую форму:
Z 1= 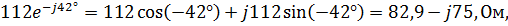
Z 1 – активно-емкостное сопротивление: R1 = 82,9 Ом; 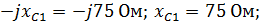
Z 2 = 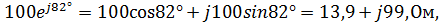
Z 2 – активно-индуктивное сопротивление: R2 = 13,9 Ом; – 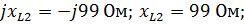
Z 3 = 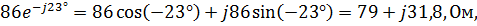
Z 3 – активно-индуктивное сопротивление: R3 = 79 Ом; – 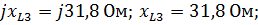
Z 4 = 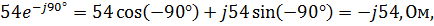
Z 4 – емкостное сопротивление: – 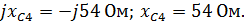
4. По исходной схеме и характеру сопротивлений составим расчетную схему цепи, рис. 2.8.
5. Расчет комплексных значений токов будем производить методом эквивалентных преобразований.
Определим сопротивление цепи (рис. 2.9). Сопротивления Z 2 и Z 4 соединены последовательно: Z 24 = Z 2 + Z 4 = 13,9 + j99 – j54 = 13,9 + j45 = 47,1  .
.

Рис. 2.9
Сопротивления Z 24 и Z 3 соединены параллельно:
Z 234 = (Z 24 Z 3)/(Z 24 + Z 3 ) = 41,1 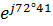 86
86 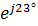 /(13,9 + j45 +79 + j31,8) = 4050,6
/(13,9 + j45 +79 + j31,8) = 4050,6  /120,5
/120,5 
Общее сопротивление цепи Z:
Z = Z 1 + Z 234 = 82,9 – j75 + 18,5 + j27,5 = 101,4 – j47,5 = 112 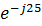 Ом.
Ом.
Ток цепи 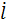 1 найдем по закону Ома:
1 найдем по закону Ома:
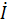 1 =
1 = 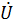 / Z = 168
/ Z = 168  /112
/112 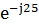 =1,5
=1,5 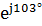 = -0,34 + j1,46, A.
= -0,34 + j1,46, A.
Для 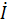 2 и
2 и 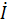 3 найдем напряжение на параллельном участке
3 найдем напряжение на параллельном участке 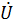 234:
234:
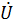 234 =
234 = 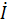 1 Z 234 = 1,5
1 Z 234 = 1,5 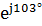 33,6
33,6 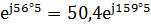 = -47 +j18, B.
= -47 +j18, B.
Токи цепи:

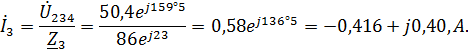
Проверим правильность расчета по первому закону Кирхгофа: 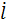 1 =
1 = 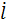 2 +
2 + 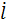 3.
3.
-0,34 + j1,46 = 0,067 + j1,06 – 0,416 + j0,40 = -0,34 + j1,46.
6. Комплексные действующие значения напряжений
- на параллельном участке:

- На последовательном участке:
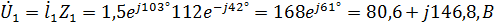 .
.
Проверим правильность расчетов по второму закону Кирхгофа: 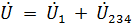 .
.
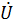 =
= 
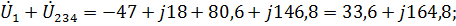
34,74 + j164,3 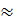 33,6 + j164,8.
33,6 + j164,8.
7. Схема включения приборов (рис. 2.9): амперметра «А» для измерения тока в неразветвленном участке цепи, вольтметра «V» для измерения напряжения на параллельном участке.
Показания приборов: A 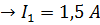 (см. значение
(см. значение 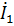 ); V
); V 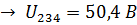 (см. значение
(см. значение  ).
).
На рис. 2.9 представлена схема включения ваттметра (W) для измерения активной мощности всей цепи. В задании ваттметр требуется включить таким образом, чтобы он измерял активную мощность только параллельного участка цепи.
Показания ваттметра: W  P =
P = 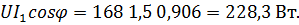
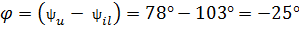 ; cos(-25
; cos(-25  ) = 0,906.
) = 0,906.
8. Баланс мощности цепи:
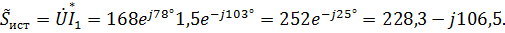
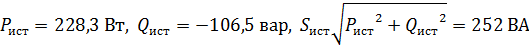 .
.
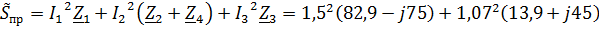
x(79 + j31,8) = 186,52 – j168,75 + 15,91 + j51,52 + 26,57 + j10,69 = 229 – j106,54 = 252,5 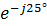
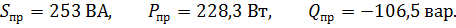
Равенство мощностей источника энергии и приемников подтверждает правильность расчета цепи.
Векторная диаграмма цепи приведена на рис. 2.10.
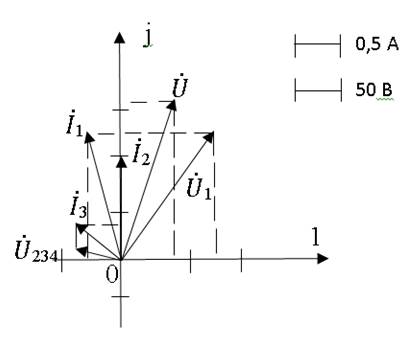
Рис. 2.10
Контрольные вопросы
1. Комплексное сопротивление цепи с последовательным соединением R = 80 Ом и xL = 60 Ом равно: в алгебраическом виде Z = , в показательном виде Z = .
2. Комплексное сопротивление цепи с сопротивлением xC = 100 Ом равно: в алгебраическом виде Z = , в показательном виде Z = .
3. Ветвь, состоящая из индуктивного сопротивления xL = 100 Ом и ветвь, состоящая из емкостного сопротивления xС = 50 Ом соединены параллельно, общее сопротивление цепи равно Z = .
4. Цепь, состоящая из ветвей пункта 3, подключена к источнику переменного напряжения 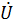 = 100 В, токи ветвей равны
= 100 В, токи ветвей равны 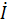 1 = ____,
1 = ____, 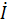 2= ___, ток в неразветвленной части цепи
2= ___, ток в неразветвленной части цепи 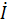 = ______.
= ______.
5. Соотношение между максимальным и действующим значением синусоидального переменного тока .
6. При построении векторных диаграмм за условно-положительное направление вращения принимается направление .
7. Синусоидальные величины с положительной начальной фазой откладываются от оси «+1» часовой стрелки.
8. Векторная диаграмма тока и напряжения ветви с активно-индуктивным сопротивлением Z = R + jxL имеет вид .
9. Векторная диаграмма тока и напряжения ветви с емкостным сопротивлением Z = -jxc имеет вид .
10. Общее сопротивление цепи с параллельным соединением ветвей с сопротивлением Z 2 и Z 3, соединенных последовательно с Z 1 равно .
11. Активная мощность цепи равна нулю, если сопротивление цепи .
12. Реактивная мощность цепи будет положительной в цепи с ________ сопротивлением.
13. В цепи с активно-емкостным соединением полная комплексная сопряженная мощность равна 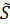 .
.
14. Комплексная мощность цепи 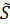 = .
= .
15. Приборы в цепях синусоидального тока показывают . значение измеряемой величины.
16. Цепь синусоидального тока с последовательным соединением R, L, C, в которой XL = XC работает в режиме .
17. Если в цепи с активно-реактивным сопротивлением преобладает емкостное сопротивление, то ток напряжение.
18. Если в цепи, состоящей из параллельно включенных сопротивлений XL и XC, cos 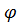 цепи = 1, то цепь будет работать в режиме .
цепи = 1, то цепь будет работать в режиме .
 2020-05-11
2020-05-11 1045
1045