Приведём другое решение

Вариант № 24592963

Задание 1 № 366810

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

 

Объекты	Хлев	Компостная яма	Баня	Жилой дом
Цифры

 

На плане изображено домохозяйство по адресу: с. Федосеево, 6-й Зелёный пер., д. 2 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок справа от ворот находится хлев, а слева — сарай, отмеченный на плане цифрой 6. Площадь, занятая сараем, равна 36 кв. м.

Жилой дом находится в глубине территории. Помимо сарая, жилого дома и хлева, на участке имеется баня, расположенная в углу участка, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Также в углу огорода расположена компостная яма.

Все дорожки внутри участка вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и сараем и сараем и хлевом имеются площадки, вымощенные такой же плиткой.

К домохозяйству подведено электричество. Имеется магистральное газоснабжение.

Решение.

При входе на участок справа от ворот находится хлев. Значит, хлев отмечен на плане цифрой 7. Компостная яма находится в углу огорода, следовательно, она отмечена на плане цифрой 1. Слева от ворот находится сарай, справа от ворот находится хлев, огород отмечен цифрой 2. Значит, баня, расположенная в углу участка, отмечена цифрой 5. Жилой дом находится в глубине участка, следовательно, он отмечен цифрой 4.

 

Ответ: 7154.

Задание 2 № 366811

Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки, а также площадки перед баней и сараем и сараем и хлевом?

 

Решение.

Заметим, что, поскольку одна плитка имеет площадь 1 м², для площадки между хлевом и сараем понадобится 120 плиток. Для площадки между баней и сараем понадобится 72 плитки. Для того чтобы выложить все дорожки, понадобится ещё 20 плиток. Значит, всего необходимо

120 + 72 + 20 = 212 плиток.

Теперь найдём, сколько упаковок плитки понадобилось:

Следовательно, чтобы выложить все дорожки и площадки понадобится 43 упаковки плитки.

 

Ответ: 43.

Задание 3 № 366812

Найдите площадь, не занятую постройками и плиткой (в м²).

 

Решение.

Площадь участка, не занятая постройками и плиткой, равна количеству клеток, умноженному на 4, поскольку сторона одной клетки равна 2 м. Значит, площадь равна:

м².

Ответ: 324.

Задание 4 № 366813

Хозяин участка планирует вырыть перед домом пруд диаметром 6 м. Найдите площадь, которую будет занимать этот пруд. Ответ дайте в виде

 

Решение.

Найдём площадь, которую будет занимать пруд:

Таким образом, получаем ответ:

 

Ответ: 9.

Задание 5 № 366816

Хозяин участка планирует провести в жилом доме отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.

 

	Нагреватель (котел)	Прочее оборудование и монтаж	Сред. расход газа / сред. потребл. мощность	Стоимость газа / электро-энергии
Газовое отопление	36 тыс. руб.	15 160 руб.	1,4 куб. м/ч	6,2 руб./куб. м
Электр. отопление	28 тыс. руб.	12 000 руб.	6,2 кВт	4,4 руб./(кВт · ч)

 

Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости оборудования и установки газового и электрического отопления?

 

Решение.

Чтобы установить газовое оборудование, понадобится 36 000 + 15 160 = 51 160 руб. Для установки электрического оборудования понадобится 28 000 + 12 000 = 40 000 руб. Разница в стоимости составляет 51 160 − 40 000 = 11 160 руб. Час обогрева газом стоит 6,2 · 1,4 = 8,68 руб./ч. Час обогрева электричеством стоит 6,2 · 4,4 = 27,28 руб./ч. Разница в стоимости составляет 27,28 − 8,68 = 18,6 руб./ч. Значит, экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления через 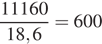часов.

 

Ответ: 600.

Задание 6 № 333111

Найдите значение выражения .

Решение.

Приведём к общему знаменателю:

 

 

Ответ: 2,18.

Задание 7 № 311392

Одно из чисел отмечено на координатной прямой точкой A. Укажите это число.

В ответе укажите номер правильного варианта.

1)

2)

3)

4)

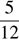
Решение.

По условию, число А лежит в интервале Определим, какой из вариантов ответа также попадает в данный интервал.

1. Поскольку числа и лежат правее данного интервала.

2. Поскольку т. к. число 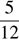лежит левее данного интервала.

3. Поскольку т. к. , число лежит в интервале

Таким образом, точка соответствует числу

 

Правильный ответ указан под номером 3.

Задание 8 № 348572

Какое из данных ниже чисел является значением выражения

1)

2)

3)

4)

Решение.

Получим значение выражения:

 

 

Ответ: 2

Задание 9 № 311381

Решите уравнение: .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение.

Используем свойство пропорции.

 

 

Ответ: 22.

Задание 10 № 311919

Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.

Решение.

Рассмотрим все возможные исходы жеребьёвки.

· Команда А в матче в обоих матчах первой владеет мячом.

· Команда А в матче в обоих матчах не владеет мячом первой.

· Команда А в матче с командой В владеет мячом первой, а в матче с командой С — второй.

· Команда А в матче с командой С владеет мячом первой, а в матче с командой В — второй.

Из четырех исходов один является благоприятным, вероятность его наступления равна 0,25.

 

Ответ: 0,25.

Задание 11 № 333008

На рисунке изображён график функции y = ax² + bx + c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

 

 

УТВЕРЖДЕНИЯ		ПРОМЕЖУТКИ
А) функция возрастает на промежутке Б) функция убывает на промежутке		1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3]

 

Ответ:

Решение.

Функция, изображённая на графике возрастает на промежутке и убывает на промежутке Следовательно, на данных промежутках функция возрастает на третьем промежутке и убывает на первом.

 

Ответ: 31.

Задание 12 № 311953

Дана геометрическая прогрессия (b_n), знаменатель которой равен 2, а . Найдите сумму первых шести её членов.

Решение.

Сумма n первых членов геометрической прогрессии даётся формулой

 

 

По условию, откуда получаем

 

 

Ответ: −47,25.

Задание 13 № 311451

Упростите выражение и найдите его значение при . В ответе запишите найденное значение.

Решение.

Упростим выражение:

 

 

 

При , значение полученного выражения равно 7,5: 5 = 1,5.

 

Ответ: 1,5.

Задание 14 № 338071

Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n = 1600? Ответ выразите в километрах.

Решение.

Найдём какое расстояние прошёл человек, подставим длину шага и число шагов в формулу:

 

 

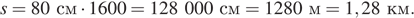
Ответ: 1,28

Задание 15 № 311385

На каком рисунке изображено множество решений неравенства ?

В ответе укажите номер правильного варианта.

 

 

1) 1

2) 2

3) 3

4) 4

Решение.

Решим данное неравенство:

 

Неравенству соответствует второй график.

 

Ответ: 2.

Задание 16 № 314980

Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

 

Перечислите эти длины в ответе без пробелов в порядке возрастания.

Решение.

Введём обозначения, как показано на рисунке. Имеем:

 

 

Тогда

 

Ответ: 1717.

Задание 17 № 340337

Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.

Решение.

Введём обозначение, как показано на рисунке. Касательные, проведённые к окружности из одной точки равны, поэтому следовательно, треугольник — равнобедренный. Откуда Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга равна 108°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 108°. Рассмотрим треугольник AOB, он равнобедренный, следовательно,

 

Ответ: 36.

Задание 18 № 169849

Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на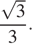

Решение.

Высота равностороннего треугольника равна Таким образом, сторона равностороннего треугольника равна Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:

 

 

Ответ: 100.

 

----------

В открытом банке иррациональный ответ.

Задание 19 № 349373

Найдите угол ABC. Ответ дайте в градусах.

Решение.

Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата стягивают равные дуги, поэтому дуга ЕАС равна 90°, а опирающийся на нее вписанный угол ЕВС равен 45°.

В треугольнике CAE проведем высоту из вершины A (см. рис.). Она разделит сторону EC пополам, поэтому треугольник CAE — равнобедренный. Тогда малые дуги EA и AC равны, так как их стягивают равные хорды. Следовательно, равны и опирающиеся на них вписанные углы ЕВА и АВС. Таким образом,

 

Ответ: 22,5.

Задание 20 № 316286

Укажите номера верных утверждений.

 

1) Если угол равен 47°, то смежный с ним равен 153°.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Через любую точку проходит ровно одна прямая.

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Если угол равен 47°, то смежный с ним равен 153°» — неверно, сумма смежных углов равна 180°.

2) «Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны» — верно, по признаку параллельности прямых.

3) «Через любую точку проходит ровно одна прямая» — неверно через одну точку проходит бесконечное множество прямых.

 

Ответ: 2.

 

Примечание.

Не следует думать, что вопрос «какие утверждения верные?» подразумевает, что в ответе должно быть несколько утверждений. Так же, как задача «решите уравнение» не подразумевает, что решение вообще есть.

Задание 21 № 311546

Один из корней уравнения равен −1. Найдите второй корень.

Решение.

Подставим известный корень в уравнение: . Получим уравнение относительно . Решим его: . Подставим уравнение: , откуда

 

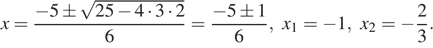
Ответ:

Задание 22 № 338847

Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько часов мальчики покрасят забор, работая втроём?

Решение.

Обозначим выполняемую мальчиками работу по покраске забора за 1. Пусть за , , часов Игорь, Паша и Володя, соответственно, покрасят забор, работая самостоятельно. Игорь и Паша красят забор за 20 часов:

 

 

Паша и Володя красят этот же забор за 24 часа:

 

,

 

а Володя и Игорь — за 30 часов:

 

 

Получаем систему уравнений:

 

 

Просуммируем левые и правые части данных трех уравнений, получим:

 

Ответ: 16.

 

Приведём другое решение.

 

За один час Игорь и Паша красят 1/20 забора, Паша и Володя красят 1/24 забора, а Володя и Игорь — за 1/30 забора. Работая вместе, за один час два Игоря, Паши и Володи покрасили бы:

 

забора.

 

Тем самым, они могли бы покрасить один забор за 8 часов. Поскольку каждый из мальчиков был учтен два раза, в реальности Игорь, Паша и Володя могут покрасить забор за 16 часов.