Изучить теорию и выполнить задания для самостоятельной работы.
Теория

Методы решения уравнений
Метод разложения на множители.
Уравнение вида 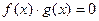 можно заменить совокупностью двух более простых уравнений
можно заменить совокупностью двух более простых уравнений 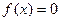 и
и 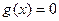 , где
, где 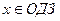 .
.
Способы разложения на множители:
- вынесение общего множителя за скобки;
- способ группировки;
- применение формул сокращенного умножения.
Пример 1. 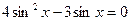
ОДЗ: x - любое число.
Вынесем за скобку множитель 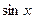 .
.
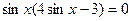
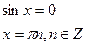
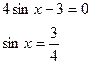
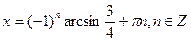
Ответ: 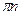 ,
, 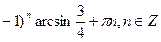
Пример 2. 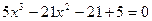 .
.
ОДЗ: х – любое число.
Сгруппируем слагаемые и вынесем общий множитель за скобки:
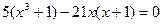
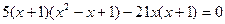
Вынесем множитель 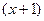 за скобку:
за скобку:
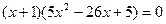
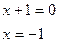
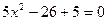 х =0,2 х =5
х =0,2 х =5
Ответ: -1; 0,2; 5.
Пример 3. 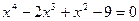 .
.
ОДЗ: х – любое число.
Сгруппируем первые три слагаемых и воспользуемся формулой квадрата разности двух чисел:
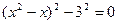
Применим формулу разности квадратов двух чисел:
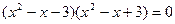
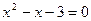
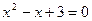
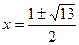 нет корней.
нет корней.
Ответ: 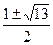 .
.
Метод введения новой переменной.
Введение новой переменной позволяет разбить задачу на подзадачи и решить вместо одного сложного несколько простых уравнений.
Пример 4. 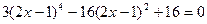
ОДЗ: х – любое число.
Замена: 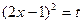 ,
, 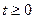
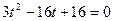

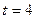 ,
, 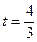
Вернемся к замене:
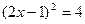
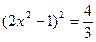
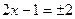
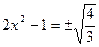
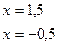
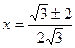
Ответ: 1,5; -0,5; 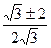 .
.
Пример 5. 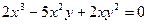
ОДЗ: х и у любые числа.
Многочлен называется однородным, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если 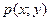 - однородный многочлен, то
- однородный многочлен, то 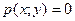 однородное уравнение.
однородное уравнение.
Вынесем общий множитель за скобки:
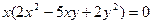
Если х =0, то у – любое число.
Если 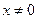 , то
, то 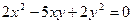 . Разделим обе части уравнения на
. Разделим обе части уравнения на 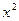 и введем новую переменную
и введем новую переменную 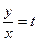 .
.
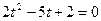
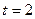
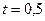
Вернемся к замене:
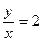
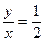
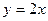
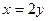
Пусть а – действительное число. Тогда ответ можно записать в виде:
(0; а), (а; 2а), (2а; а).
Пример 6. 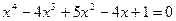
ОДЗ: х – любое число.
Многочлен называют симметрическим, если коэффициенты членов, равно отстоящих от концов, равны между собой. Для многочленов с двумя переменными - если при одновременной замене х на у и у на х, многочлен сохраняет свой вид. Например,  .
.
Разделим обе части данного уравнения на 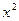 .
.
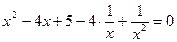
Сгруппируем 1 и 5 слагаемое, 2 и 3 слагаемое:
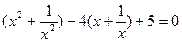
Пусть 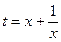 , тогда
, тогда 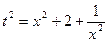 , а
, а 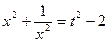
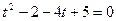
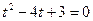
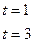
Вернемся к замене:
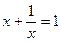
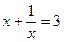
Решив эти уравнения, получаем корни 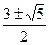 .
.
Ответ: 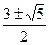
Метод деления на многочлен.
Этот метод применяют при решении уравнений высших степеней. Цель – понизить степень многочлена.
Пример 7. 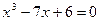
ОДЗ: х – любое число.
Выпишем делители свободного члена многочлена:
±1; ±2; ±3; ±6.
Число 1 обращает многочлен в 0. Значит х =1 – корень уравнения.
Разделим многочлен 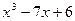 на двучлен
на двучлен 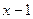 . Получим
. Получим 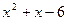 .
.
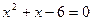
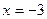
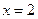
Ответ: 1; -3; 2.
2. Избавление от знаменателя.
Для того чтобы избавиться от знаменателя необходимо умножить обе части уравнения на общий знаменатель. Этот тип уравнений требует собой осторожности, т.к. найденные корни могут обращать знаменатель в 0.
Пример 8. 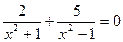
ОДЗ: 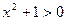 при любом х,
при любом х, 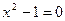 при
при 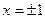
Умножим обе части уравнения на 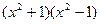
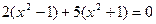
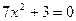
Уравнение не имеет решения.
Ответ: нет корней.
 2020-05-11
2020-05-11 161
161







