Правила нахождения точек перегиба

1) Найти вторую производную функции.

2) Найти критические точки второго рода.

3) Исследовать знак второй производной в промежутках, на которые найденные критические точки делят область определения функции.

4) Определить точки перегиба и найти значение функции в этих точках.

На этом уроке мы должны научиться проводить исследование функций и строить их графики. Исследование функции на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции f и ее критические точки, а затем выясняют, какие из них являются точками экстремума.

Для полного исследования функции f и построения ее графика удобно пользоваться общей схемой исследования, которая состоит из следующих пунктов:

Найти области определения и значений данной функции f.

Выяснить, обладает ли функция особенностями, облегчающими исследование, то есть является ли функция f:

а) четной или нечетной;

б) периодической.

3. Вычислить координаты точек пересечения графика с осями координат.

4. Найти промежутки знакопостоянства функции f.

5. Выяснить, на каких промежутках функция f возрастает, а на каких убывает.

6. Найти точки экстремума (максимум или минимум) и вычислить значения f в этих точках.

7. Исследовать поведение функции f в окрестности характерных точек не входящих в область определения.

8. Построить график функции.

Эта схема имеет примерный характер.

Учитывая все сказанное, исследуем функцию: f(x)= 3x⁵-5х³+2 и построим ее график.

Проведем исследование по указанной схеме:

D (f ') =IR, так как f (x) - многочлен.

Функция f не является ни четной, ни нечетной, так как

f (-x)= 3(-x)⁵-5(-x)³+2 = -3x ⁵+5х³+2= -(3x⁵-5х³-2) 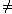f(x)

Найдем координаты точек пересечения графика с осями координат:

а) с осью 0Х, для этого решим уравнение: 3x⁵-5х³+2 = 0.

Методом подбора можно найти один из корней (x = 1). Другие корни могут быть найдены только приближенно. Поэтому для данной функции остальные точки пересечения графика с осью абсцисс и промежутки знакопостоянства находить не будем.

б) с осью 0У: f(0)=2

Точка А (0; 2) - точка пересечения графика функции с осью 0У.

Отметили, что промежутки знакопостоянства не будем находить.

Найдем промежутки возрастания и убывания функции

а) f '(x)= 15x⁴-15х² = 15х² (х²-1)

D (f ') =IR, поэтому критических точек которых f '(x)не существует, нет.

б) f '(x) = 0, если х²(х²-1)=0 <=> x = -1 V x = 0 V x = 1.

в) Получим три критические точки, они разбивают координатную прямую на четыре промежутка. Определим знак производной на этих промежутках:

Рис.3 (знаки f ')

Из рисунка 3 видно, что: f возрастает на интервалах (- ; -1) и (1; + );

f убывает на (-1; 0) и (0; 1).

Так как функция непрерывна в точках -1; 0; 1, то f возрастает на (- ; -1] и [1; + );

f убывает на [-1; 0] и [0; 1].

6. Найдем точки экстремума функции и вычислим значения функции в этих точках. Рассматривая рисунок 3 знаков f?видим, что:

x =-1 - точка max, f (-1) =4;

x = 1 - точка min, f (1) =0.

Полученные результаты занесем в таблицу и построим график

- Исследуйте функцию и постройте ее график: f (x)= x⁴-2х²-3.

Ученик: - 1) D (f) =R.

2) f(-x)= (-x)⁴-2(-x)²-3 = x ⁴-2х²-3; f(-x)= f(x),

значит, функция f является четной. Исследование ее можно проводить на промежутке [0; ).

3) Найдем точки пересечения графика функции с осями координат, то есть решим уравнение x ⁴-2х²-3 = 0. Пусть х² =у, у²-2у-3= 0, у=3 или у=-1, то есть х²=3, х= 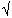3 или х=- 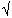3; х²=-1 не имеет решений. Получили две точки пересечения с осью абсцисс М( 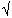3; 0), К(- 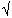3; 0). График пересекает ось ординат в точке В (0; -3).

4) Найдем производную f '(x) = 4x ³-4х = 4х(х-1)(х+1).

5) Найдем критические точки функции:

а) f ''(x) =0, если 4х (х-1) (х+1)=0, <=> x = 0 V x = -1 V x = 1.

б) f ' определена на всей D(f).

6) Определим знак производной на промежутках (- ; -1), (-1; 0), (0; 1), (1; ):

а) f '(2) = -32+8 < 0;

б) f '(-1/2) = 4 * (-1/2)³ -4 * (-1/2)= -1/2 + 2 > 0;

в) f '(1/2) = 4 * (1/2)³ -4 * (1/2)= 1/2 - 2 < 0;

г) f '(2) = 4 * 8 - 4 * 2 > 0.

Найдем значения функции в точках -1; 0; 1:

f (-1)=-4, f(0)=-3, f(1)=-4.

Полученные данные занесем в таблицу:

x	(- ; -1)	-1	(-1; 0)	0	(0; 1)	1	(1; )
f ''(x)	-	0	+	0	-	0	+
f (x)	убывает	-4	возрастает	-3	убывает	-4	возрастает
		min		max		min

Построим график.

Пример: - Найти число корней уравнения: 2x ³-3x ²-12х-11=0

Решение: Рассмотрим функцию f(x)= 2x ³-3x ²-12х-11=0.

Найдем область определения функции: D (f) = (- ; )

Найдем ее производную: f '(x) = 6x ²-6х-12

Найдем критические точки функции:

f '(x) =0, если 6x ²-6х-12=0, <=> x = -1 V x = 2.

Заполним таблицу:

x	(- ; -1)	-1	(-1; 2)	2	(2; )
f ''(x)	+	0	-	0	+
f (x)	возрастает	-4	убывает	-31	возрастает
		max		min

5) а) На промежутке (- ; -1] функция возрастает от - до -4, поэтому на этом промежутке уравнение f (x)=0 корней не имеет.

б) На промежутке [-1; 2] уравнение так же не имеет корней, так как на этом промежутке функция убывает от -4 до -31.

в) На промежутке [2; ) функция возрастает от -31 до бесконечности, на этом промежутке уравнение f (x)=0 имеет один корень (по теореме о корне, то есть если функция возрастает (убывает) на промежутке I, число а - любое из значений, принимаемых f на этом промежутке, то уравнение f (x) = а имеет единственный корень в промежутке I). Итак, уравнение 2x³-3x ²-12х-11=0 имеет один корень и этот корень принадлежит интервалу (2; ).

Учитель: - Сколько корней имеет уравнение: x ⁴/4 -x ³- x ²/2 +3х = 0

Ученик: - Решение: Рассмотрим функцию р(x) = x ⁴/4 -x ³- x ²/2 +3х:

1) Найдем область определения функции D(р) = (- ; ).

2) Найдем производную р' (x) = x ³- 3x ² -x+3

3) Найдем критические точки и промежутки возрастания и убывания функции:

р' (x) = 0 <=> x ³- 3x ² -х+3=0 <=> x ²(х-3) -(х-3)=0 <=> (х-3)(x ²-1) = 0 <=> х=3, х₁=1, х₂=-1.