2020-05-12
223
Вторая производная, ее геометрический и физический смысл.
Цель занятия:
Должен уметь: находить промежутки возрастания и убывания функции используя вторую производную. Находить точки экстремума.
Должен знать: Применение второй производной к нахождения промежутков монотонности.
Пусть функция 
– дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
Если найти производную от функции 
, получим вторую производную функции .
т.е. 
или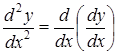 
.
Этот процесс можно продолжить и далее, находя производные степени n.
.
Исследование функции на экстремум с помощью производной второго порядка.
Теорема 5. Если 
, то функция в точке х 0 имеет максимум, если 
и минимум, если 
.
Если 
, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.
Выпуклость и вогнутость кривой. Точки перегиба.
Кривая обращена выпуклостью вверх на интервале 
, если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
|
|
|
Теорема 6. Если функция имеет на интервале вторую производную и 
() во всех точках данного интервала, то график функции имеет на выпуклость, направленную вниз (вверх).
Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба. Точками перегиба могут служить только критические точки второго рода, т.е. точки, в которых вторая производная 
обращается в ноль или не существует.
Теорема 7. Пусть кривая определяется уравнением 
. Если вторая производная 
или не существует и при переходе через точку 
меняет знак, то точка кривой с абсциссой является точкой перегиба.
