Показатели вариации признака

 

Для характеристики статистических распределений обычно используется три группы обобщающих показателей:

1). Показатели центра распределения – определяют среднее значение признака в вариационном ряду. Для этой цели в основном используются средняя арифметическая, мода и медиана.

2). Показатели степени вариации – определяют степень колеблемости отдельных значений признака.

3). Показатели формы распределения – определяют степень симметричности и однородности распределения.

Вариация признака в ряду распределения характеризуется рядом абсолютных и относительных показателей.

Абсолютные показатели вариации:

1). Размах вариации (R) характеризует границы вариации изучаемого признака и вычисляется по формуле:

,

где x_max и x_min – наибольшее и наименьшее значения варьиру­ющего признака.

Размах вариации показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака. Показатель основан на крайних значениях варьирующего признака и не отражает отклонений всех вариант в ряду. Повторяемость промежуточных значений здесь не учитывается.

Этот показатель представляет интерес в тех случаях, когда важ­но знать, какова амплитуда колебаний значений признака, на­пример, каковы колебания цены на данный товар в течение неде­ли или по разным регионам в данный отрезок времени.

Однако этот показатель не даёт представления о характере вариационного ряда, расположении вариантов вокруг средней и может сильно меняться, если добавить или исключить крайние варианты (когда эти значения аномальны для данной совокуп­ности). В этих случаях размах вариации даёт искаженную амплиту­ду колебания против нормальных её размеров. В связи с этим следует очистить совокупность от аномальных наблюдений, прежде чем определять размах вариации.  Гораздо более точной будет характеристика вариации, если показатель будет учитывать отклонения каждой из вариант от средней величины.

Для оценки колеблемости значений признака относительно средней используются характеристики рассеяния. Они различают­ся выбранной формой средней и способами оценки отклонений от неё отдельных вариантов.

2). Среднее линейное отклонение () есть средняя арифметическая из абсолютных значений отклонений отдельных вариантов от их средней величины:

	для несгруппированных данных
	для сгруппированных данных

где x_i - значение признака в дискретном ряду или середина ин­тервала в интервальном распределении;

f_i  - частота признака.

Среднее линейное отклонение даёт обобщающую характеристику распределению отклонений, учитывает различие всех единиц изучаемой совокупности. Оно не зависит от случайных колебаний вариант.

Среднее линейное отклонение выражено в тех же единицах из­мерения, что и варианты или их средняя. Оно даёт абсолютную меру вариации, показывает, на какую величину отклоняется признак в изучаемой совокупности от средней величины признака.

Порядок расчёта среднего линейного отклонения:

1) по значениям признака исчисляется средняя арифметическая:

2) определяются отклонения каждой варианты  от средней: ;

3) рассчитывается сумма абсолютных величин отклонений: ;

4) сумма абсолютных величин отклонений делится на число значений: .

Показатель среднего линейного отклонения нашёл широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования.

Но, к сожалению, этот показатель усложняет расчёты вероятностного типа, затрудняет применение методов математической статистики. Чтобы избежать равенства нулю суммы отклонений от сред­ней, используют либо абсолютные значения отклонений, либо их чётные степени, например, квадраты.

3). Дисперсия (s²) представляет собой среднюю арифметическую квадратов отклонений индивидуальных значений признака от их средней величины. Дисперсия обычно называется средним квадратом отклонений. В зависимости от исходных данных вычисляется по формулам:

	для несгруппированных данных
	для сгруппированных данных

 

Порядок расчёта дисперсии:

1) определяют среднюю арифметическую: ;

2) определяются отклонения вариант от средней ;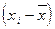

3) возводят в квадрат отклонение каждой варианты от средней ;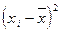

4) суммируют квадраты отклонений: ;

5) полученную сумму делят на число значений: .

Расчёт дисперсии может быть упрощён.

или

Дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.

Порядок расчёта дисперсии:

1) определяют среднюю арифметическую ;

2) возводят в квадрат среднюю арифметическую ;

3) возводят в квадрат каждую варианту ряда ;

4) находим сумму квадратов вариант ;

5) делят сумму квадратов вариант на их число, т. е. определяют средний квадрат ;

6) определяют разность между средним квадратом признака и квадратом средней .

Свойства дисперсии:

1) дисперсия постоянной величины равна нолю;

2) уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет:  (это значит, что дисперсию можно вычислить не по заданным значениям признака, а по их отклонениям от какого-то постоянного числа, например, от условного нуля);

3) уменьшение или увеличение весов (частот) варьирующего признака в определённое число раз дисперсии не изменяет;

4) уменьшение или увеличение каждого значения признака в какое-то число раз (k раз) соответственно уменьшает или увеличивает дисперсию в  раз: ;

5) дисперсия признака относительно произвольной величины А всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: 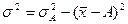. Дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин (свойство минимальности).

Каждое свойство при расчёте дисперсии может быть применено самостоятельно или в сочетании с другими.

В интервальных рядах распределения возникает систематическая ошибка дисперсии, вызванная применением сгруппированных данных. В этом случае дисперсию следует уменьшить на 1/12 квадрата величины интервала. Это значение получило название поправка Уильяма Флитвуда Шеппарда (1863-1936). Её следует учитывать при анализе признаков с непрерывным характером вариации и при большом исходных данных (более 500).

Среди варьирующих признаков, которые изучает статистика, встречаются признаки вариации, которые проявляются в том, что у одних единиц совокупности они встречаются, у других нет. Их называют альтернативными.

Альтернативные признаки – два противоположных, взаимоисключающих друг друга качественных признака, которыми одни единицы совокупности обладают (значение варианта 1), а другие не обладают (значение варианта 0) (например, пол – мужской и женский, население – городское и сельское, продукция – годная и бракованная).

Количественно вариация альтернативного признака в численности всей совокупности обозначается  а доля единиц, не обладающих признаком, обозначается 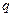 и принимает значения , тогда:                

Среднее значение альтернативного признака равно доле, которая является обобщающей характеристикой совокупности по этому варьирующему признаку:

Тогда дисперсия альтернативного признака равна:

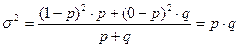
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, не обладающих этим признаком. Т. к. , то средний квадрат отклонений не может быть больше 0,25:

;

Вследствие суммирования квадратов отклонений дис­персия даёт искажённое представление об отклонениях, измеряя их в квадратных единицах.

4). Среднее квадратическое отклонение (s) – это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Она измеряется в тех же единицах, что и варьирующий признак, и исчисляется путём извлече­ния квадратного корня из дисперсии:

	для несгруппированных данных
	для сгруппированных данных

 

Среднее квадратическое отклонение, как и среднее линейное отклонение, показывает, насколько в среднем отклоняются кон­кретные варианты признака от его среднего значения.

Среднее квадратическое отклонение является мерилом надёжности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность. Величина s часто используется в качестве единицы измерения отклонений от средней арифметической. Отклонение, выраженное в s, называ­ется нормированным или стандартизированным.

Если распределение признака близко к нормальному или симметричному, то по правилу мажорантности (т. к. среднее квадратическое отклонение – средняя геометрическая величина, а среднее линейное отклонение – средняя арифметическая) среднее квадратическое отклонение больше среднего линейного отклонения (), причём: , .

 

Относительные показатели вариации устанавливают соотношение абсолютных показателей вариации признака и средней арифметической (или медианы):

1). Коэффициент осцилляции определяется как отношение размаха вариации к средней величине признака и характеризует относительную рассеянность или колеблемость крайних значений признака вокруг средней:

,

где 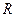 – размах вариации.

Этот показатель показывает, на сколько процентов отклоняется средняя от крайних значений вариации.

Если >100, то  (крайних значений признака), и наоборот.

2). Относительное линейное отклонение(линейный коэффициент вариации) – среднее линейное отклонение делится на среднюю величину:

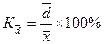
Относительное линейное отклонение характеризует долю усреднённого значения абсолютных отклонений от средней величины.

3). Коэффициент вариации (квадратический) – это наиболее распространённый показатель колеблемости, используемый для оценки типичности средних величин, представляет собой отношение среднего квадратического отклонения к среднему значению:

 

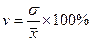
Коэффициент вариации даёт относительную оценку вариации значений признака вокруг средней величины. Значения коэффициента вариации изменяются от 0 до 1, и чем ближе он к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности, а значит и качественнее подобраны статистические данные.

Коэффициент вариации применяется в следующих случаях:

- когда необходимо определить и сравнить степени распределения двух или нескольких признаков, выраженных в различных единицах измерения для характеристики одной и той же совокупности;

- когда необходимо определить распределение одного и того же признака в разных совокупностях, имеющих разные единицы измерений и разные средние величины;

- для характеристики однородности статистической совокупности.

Если коэффициент вариации составляет более 33%, то такая совокупность считается неоднородной, а средняя нетипичной. Чем коэффициент меньше, тем однороднее совокупность, а средняя точнее отображает значения варьирующего признака.

Обычно коэффициент вариации несколько (примерно на 25%) больше линейного отклонения, если они рассчитаны по одним и тем же данным.

Таблица 2.2. Показатели вариации

	Показатель	Формула расчёта показателя
		простой	взвешенный
Абсолютные	Размах
	Среднее линейное отклонение
	Дисперсия	σ2
	Среднее квадратическое отклонение
относительные	Коэффициент вариации
	Линейный коэффициент вариации
	Коэффициент осцилляции

Пример 1.

Имеются данные о стаже работы рабочих трёх бригад:

I бригада – 15, 18, 20, 22, 25 лет;

II бригада – 10, 15, 20, 25, 30 лет;

III бригада – 8, 12, 17, 25, 38 лет.   

Определить показатели вариации.

 

1. Размах вариации.

 

2. Среднее линейное отклонение.

I.    

II.  

III.  

 

В I бригаде абсолютное отклонение каждого значения от средней величины 2,8 лет, во II бригаде – 6 лет, в III бригаде – 9,2 лет.

 

 

3. Дисперсия, среднее квадратическое отклонение.

 

I.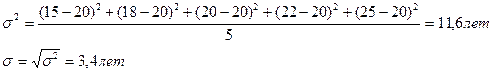

II.

III.

Чем больше среднее квадратическое отклонение, тем более высока вариация, т. е. более неточным будет среднее значение.

 

4. Коэффициент вариации.

I.

II.

III.

 

II и III бригады являются неоднородными совокупностями, т. к.  их коэффициенты вариации составляют более 0,33.

 

Пример 2.

Рассчитать абсолютные показатели вариации и показатели относительного рассеивания по данным таблицы.

Выполнение нормы, %	Среднее значение, %	Численность рабочих, чел.
80-90	85	5
90-100	95	19
100-110	105	36
110-120	115	25
120 и более	125	15
Итого:		100