2020-05-11
104
При создании математической модели движения ДА руководствуются следующими исходными предпосылками:
• уровень сложности модели должен отражать степень априорной информированности о характеристиках объекта, полученных на стадии его предшествующих исследований, а также о параметрах среды и гравитационного поля планеты;
• структура модели должна допускать ее последующее упрощение (либо усложнение по мере уточнения используемой априорной информации) в зависимости от характера решаемых задач;
• форма записи уравнений движения должна быть такой, при которой обеспечивается минимизация времени, затрачиваемого на численное интегрирование в пределах одного шага вычислений.
Как показали исследования, указанным требованиям удовлетворяет математическая модель движения, кинематические и динамические уравнения центра масс которой записываются в осях местной географической системы координат, а уравнения моментов – относительно главных осей инерции аппарата [22].
Введем следующие обозначения:
|
|
|
, 
, 
– орты местной системы координат, ориентированные соответственно на север, вертикально вверх и на восток;
, 
, 
– орты инерциальной системы координат;
– система главных осей инерции аппарата;
– система осей аэродинамической симметрии с центром на оси симметрии формы;
– радиус Земли;
– гравитационное ускорение на поверхности Земли;
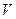– скорость полета;
– угол между горизонтальной проекцией скорости и ортом 
;
– угол наклона скорости к местному горизонту;
, 
, 
– углы курса, тангажа и крена аппарата относительно ортов oсей 
, 
, 
;
– широта;
– долгота;
, 
, 
– проекции орта местной вертикали на оси , 
, 
;
, 
, 
– проекции орта 
на оси аэродинамической симметрии;
, 
… 
– проекции векторов 
, 
, 
на оси, параллельные осям 
;
– матрица направляющих косинусов ортов главных осей инерции относительно центральных осей, параллельных осям ;
, 
, 
– проекции вектора скорости в неподвижной системе координат;
, 
, 
– составляющие угловой скорости в главных осях инерции:
, 
, 
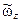– проекции вектора угловой скорости на оси ;
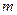– масса аппарата;
, 
, 
– главные моменты инерции аппарата;
– площадь миделя;
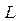– характерный размер аппарата;
– проекция кратчайшего отрезка между продольной осью 
и
центром масс аппарата на ось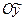 
;
; 
, если центр масс расположен ниже оси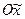 
;
– проекция кратчайшего отрезка между продольной осью 
и
центром масс аппарата на ось 
;
, если центр масс находится справа, по ходу от плоскости 
;
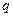– скоростной напор;
– плотность атмосферы;
, 
, 
– моменты, создаваемые органами управления;
– высота полета аппарата над поверхностью сферы радиусом 
;
|
|
|
– коэффициент аэродинамической силы, действующей вдоль оси
аэродинамической симметрии 
(
при 
);
– коэффициент аэродинамической силы, действующей в плоскости, проходящей через вектор скорости и ось 
(плоскость пространственного угла атаки) перпендикулярно оси ;
– приведенная характеристика поперечной силы:
; (4.1)
– коэффициент продольного демпфирующего момента, действующего в плоскости угла атаки, относительно основания перпендикуляра, опущенного из центра масс на ось симметрии;
– приведенная характеристика продольного момента (вектор момента перпендикулярен плоскости пространственного утла атаки)
; (4.2)
– коэффициент продольного демпфирующего момента, действующего в плоскости пространственного утла атаки (
– проекция вектора 
на нормаль к плоскости угла атаки);
– коэффициент «бокового» демпфирующего момента (
– проекция вектора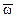 
на плоскость угла атаки);
, 
, 
– перегрузки, действующие в центе масс аппарата, параллельно осям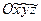 
.
Углы 
, 
, 
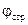указывают на ориентацию осей чувствительности измерительных приборов и направления действия струйных органов управления, если такие устройства рассматриваются в задаче.
В принятых обозначениях система уравнений движения аппарата запишется следующим образом:
|
|  ;
| (4.3) |
 ;
| ||
 ;
|
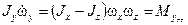т.е. 
, (4.4)
где 
;
;
,
где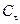 
, 
, , 
– функции 
или 
.
В свою очередь: 
, (4.5)
|
|  ;
| (4.6) |
 ;
| ||
|
| где |  ;
|
|  ;
| |
 ;
|  ;
| |||
 ;
|  ;
|
|
|  ;
|
|  ;
| |
 ;
|  ;
| |||
 ;
|  ;
|
| 
|
| 
|
| 
|
|  .
|
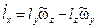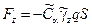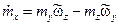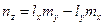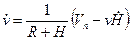
Показано, что блочный принцип построения опорной модели дает возможность использовать ее модификации для расчета движения центра масс аппарата и его движения относительно центра масс как раздельно, так и в рамках единой модели, а также при проведении расчетов на участке активного торможения. В сочетании с применением универсальных методов численного интегрирования (классический вариант метода Рунге–Кутта и его разновидности) и использовании результатов экспериментальных аэродинамических исследований модель позволяет проводить углубленный количественный анализ аэробаллистических схем и осуществлять обоснованный анализ при выборе рациональных вариантов конструктивно-компоновочных схем ДА.
Наиболее известными и широко применяемыми средствами дополнительного аэродинамического торможения, предназначенными для большего снижения скорости аппарата при посадке на поверхность планеты, являются ПС [23–24]. Проблемы, связанные главным образом с вводом в действие ПС при больших скоростных напорах набегающего потока, и наоборот, при малых скоростных напорах (недостаточных для наполнения) в условиях разреженных атмосфер, сложные динамические условия, сложности математического моделирования и экспериментальной отработки многозвенных, мягких тканевых конструкций и т.д., привели к необходимости рассмотрения альтернативных конструкций. К таковым в первую очередь относятся разворачиваемые жесткие или полужесткие конструкции зонтичного типа. Развитие технологии надувных тормозных устройств привело к расширению возможностей и к новым решениям при формировании схем десантирования в атмосфере. Следует отметить, что независимо от типа применяемых конструкций, при проведении проектных оценок могут использоваться одни и те же уравнения движения и схемные решения.
Размерно - массовые модели тормозных устройств могут различаться даже внутри одного класса или типа используемых средств. Диаметр лобового экрана ограничен размерами обтекателя ракеты-носителя. Рассматривался вариант использования ракеты-носителя «Протон» с допустимым диаметром миделя экрана 4,26 м. ТЗУ в раскрытом состоянии имело диаметр около 12 м. НТУ пенетратора 2,3-3,8 м., устройства для тяжелых ДА – 22 м. ПС различного назначения имеют, соответственно, различные размеры, например: вытяжной парашют – 0,5 м, стабилизирующий парашют – 1-7 м, тормозной – 10-50 м, основной – 50-500, 1000 м. и т.д. Массы доставляемых на поверхность планет средств составляют:
|
|
|
· марсианской мини-станции, малой станции и пенетратора – 20-100 кг;
· ДА с исследовательской лабораторией (марсоходом, аэростатным зондом) или взлетной ракетой для доставки грунта на Землю – при входе в атмосферу – 1000-5000 кг;
· ДА для доставки пилотируемой экспедиции на Марс – 70000 кг.
Для сравнения приведем размеры венерианской и марсианской дрейфующих аэростатных станций. Диаметр первой в форме сферы составлял 3,5 м., а размеры второй, в форме цилиндра, составляли: диаметр 13 м., а длина 42 м. Массы АЗ были одного порядка. Конечно, главная причина такой разницы – большая разреженность атмосферы Марса, но, как было показано в ходе работ, для ввода в действие этих средств исследований могут быть использованы идентичные схемные решения [25, 27–31].
