Практическая работа №90 Прикладные задачи
Тест
1. В коробке 4 белых и 6 серых лабораторных мышей. Какова вероятность не глядя достать из коробки не белую мышь?
а) 0,4
б) 0,2
в) 0,6
г) 0,24
2. Из той же самой коробки подряд вынимают две мыши. Какова вероятность, что первая будет белая, а вторая серая?
а) 4/15
б) 0,24
в) 0,16
г) 0,36
3. В двух коробках по 1 альбиносу и по 9 обычных лабораторных мышей. Вынимая из каждой коробки по одной, какова вероятность получить двух альбиносов?
а) 0,1
б) 0,01
в) 0,9
г) 0,81
4. На первую подстанцию скорой помощи поступает вызов с вероятностью 0,9, а на вторую 0,8. Какова вероятность, что вызов поступит хотя бы на одну подстанцию?
а) 0,98
б) 0,72
в) 0,02
г) 0,18
5. * На подстанции 3 врача и 5 фельдшеров. Бригада из трех человек формируется случайным образом. Какова вероятность, что в ней будет 1 врач и 2 фельдшера?
а) 0,6
б) 2/15
в) 15/28
г) 3/8
Урок 2. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы
Составить таблицу
| Уравнения | Определение | Способ решения/алгоритм |
Рациональные уравнения – это уравнения, в которых и левая, и правая части рациональные выражения.
Если в дроби нет деления на переменную, тогда рациональное уравнение будет называться целым (или линейным) уравнением.
Алгоритм правильного решения рациональных уравнений
- Понять, точно ли перед тобой рациональное уравнение (убедись, что в нем нет корней);
- Определить ОДЗ;
- Найти общий знаменатель дробей и умножить на него обе части уравнения;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль знаменатель дробей.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня.
Иррациональное уравнение, как правило, сводится к равносильной системе, содержащей уравнения и неравенства.
1. 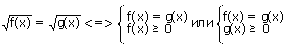
Из двух систем выбирают ту, которая решается проще.
2. 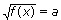
Если а < 0, уравнение не имеет корней.
Если 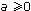 , уравнение равносильно уравнению
, уравнение равносильно уравнению 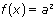 .
.
3. 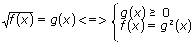
Иррациональные уравнения могут быть также решены путем возведения обеих частей уравнения в натуральную степень. При возведении уравнения в степень могут появится посторонние корни. Поэтому необходимой частью решения иррационального уравнения является проверка.
При решении иррациональных уравнений, как правило, используют следующие методы:
1) переход к равносильной системе (в этом случае проверка не нужна);
2) метод возведения обеих частей уравнения в одну и ту же степень;
3) метод введения новых переменных.
Если вы не следите за равносильностью переходов, то проверка является обязательным элементом решения. О.Д.З. в иррациональных уравнениях не поможет Вам отсеять все посторонние корни. Обратите на это внимание!
При решении иррациональных уравнений, как правило, используют следующие методы: 1) переход к равносильной системе (в этом случае проверка не нужна); 2) метод возведения обеих частей уравнения в одну и ту же степень; 3) метод введения новых переменных.
Примеры.
1. 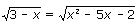
Решение:
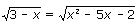 | <=> | 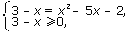 | <=> | 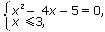 | <=> | 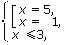 | <=> |
| <=> x = -1 |
Ответ: -1.
Показательными называются уравнения, в которых неизвестное содержится в показателе степени. Простейшее показательное уравнение имеет вид: ах = аb, где а> 0, а  1, х - неизвестное.
1, х - неизвестное.
Основные свойства степеней, при помощи которых преобразуются показательные уравнения: а>0, b>0.
1. а0 = 1, а1= а.
2. аm/n= 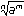 , где m и n– натуральные числа.
, где m и n– натуральные числа.
3. a-n = 1/ аn
4. an × am = an+m
5. an/am = an-m
6. (an)m = an-m
7. (ab)n = an×bn
8. (a/b)n = an/bn.
При решении показательных уравнений пользуются также следующими свойствами показательной функции: y = ax, a > 0, a  1:
1:
1. ax>0, при всех a>0 и x  R;
R;
2. 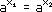
 x1 =x2.
x1 =x2.
Для представления числа в виде степени используют основное логарифмическое тождество: b = 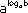 , a > 0, a
, a > 0, a  1, b > 0.
1, b > 0.
Для успешного решения показательных уравнений Вы должны знать основные свойства степеней, свойства показательной функции, основное логарифмическое тождество.
При решении показательных уравнений используют два основных метода:
1. переход от уравнения af(x) = ag(x) к уравнению f(x) = g(x);
2. введение новых прямых.
Примеры.
1. Уравнения, сводящиеся к простейшим. Решаются приведением обеих частей уравнения к степени с одинаковым основанием.
3x = 9x – 2.
Решение:
3x = (32)x – 2;
3x = 32x – 4;
x = 2x –4;
x = 4.
Ответ: 4.
Простейшие тригонометрические уравнения.
1. sinx = a, |a| 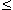 1
1
x = (–1) k arcsin a +  k, k
k, k 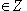
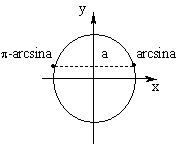
Частные случаи:
| a = –1 | a = 0 | a = 1 |
| sinx = –1 | sin x = 0 | sin x = |
x = – 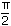 + 2 + 2  k, k k, k 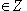 | x =  k, k k, k 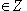 | x = 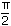 + 2 + 2  k, k k, k 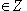 |
 |  |  |
| | a| >1 корней нет |
2. cos x = a, |a| 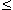 1
1
x = ± arccos a + 2  k, k
k, k 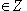
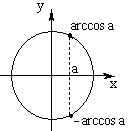
Частные случаи:
| a = –1 | a = 0 | a = 1 |
| cos x = –1 | cos x = 0 | cos x = 1 |
x =  + 2 + 2  k, k k, k 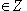 | x = 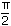 + +  k, k k, k 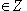 | x = 2  k, k k, k 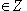 |
 |  |  |
| |a| >1 корней нет |
3. tg x = a, a 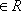
x = ± arctg a +  k, k
k, k 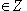
Основные типы тригонометрических уравнений.
1. Уравнения, сводящиеся к простейшим.
2. Уравнения, сводящиеся к квадратным.
3. Однородные уравнения: asinx + bcosx = 0, a sin 2 x + b sinxcosx + c cos 2 x = 0.
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
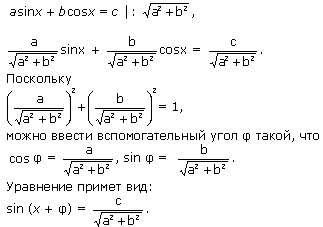
5. Уравнения, решаемые разложением на множители.
6. Нестандартные уравнения.
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
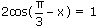
Решение:
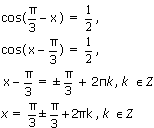
Ответ:
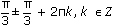
 2020-05-11
2020-05-11 2006
2006






