Тема: «Векторы в пространстве. Равенство векторов»
Теория
Отрезок, для которого указано, какой из его концов считать началом, а какой – концом, называется вектором. Направление вектора от начала к концу отмечено стрелкой. Любая точка пространства может также рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Нулевой вектор обозначается  .
.
Длиной ненулевого вектора  называется длина отрезка АВ. Длина вектора
называется длина отрезка АВ. Длина вектора  обозначается так
обозначается так  . Длина нулевого вектора считается равной нулю:
. Длина нулевого вектора считается равной нулю:  .
.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора  и
и  коллинеарны и если при этом лучи АВ и СD сонаправлены, то векторы
коллинеарны и если при этом лучи АВ и СD сонаправлены, то векторы  и
и  называются сонаправленными
называются сонаправленными  , а если эти лучи не являются сонаправленными, то векторы
, а если эти лучи не являются сонаправленными, то векторы  и
и  называются противоположно направленными
называются противоположно направленными  . Нулевой вектор считается сонаправленным любому вектору.
. Нулевой вектор считается сонаправленным любому вектору.
Векторы называются равными, если они сонаправлены и их длины равны.

От любой точки можно отложить вектор, равный данному, и притом только один.
Примеры
Пример 1: Измерения прямоугольного параллелепипеда АВСDEMKF таковы: АD=13 см, АВ=6 см, АE=10 см. Найдите длины векторов: СK, EM, AK, BC, EF, FK.

Решение: CK=AE, 
EM=AB, 


BC=AD, 
EF=AD, 
FK=AB, 
Пример 2: Дан прямоугольный параллелепипед АВСDEMKF. Установить, какие из данных векторов равны

Решение:

Самостоятельная работа
1) Измерения прямоугольного параллелепипеда АВСDA1B1C1D1 таковы: DC=5 см, ВC=7 см, АA1=11 см. Найдите длины векторов: BB1, AB, D1C1, DB1, AC1, B1C1.
2) Дан прямоугольный параллелепипед АВСDA1B1C1D1. Установить, какие из данных векторов равны

Тема: «Операции над векторами. Разложение вектора»
Теория
Пусть даны два произвольных вектора 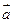 и
и  . Отложим от какой-нибудь точки А вектор
. Отложим от какой-нибудь точки А вектор  , равный
, равный 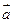 . Затем, от точки В отложим вектор
. Затем, от точки В отложим вектор  , равный
, равный  . Вектор
. Вектор  называется суммой векторов
называется суммой векторов 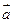 и
и  :
:  . Это правило сложения векторов называется правилом треугольника. Оно может быть также сформулировано и в другой форме: для любых трех точек А, В и С имеет место равенство
. Это правило сложения векторов называется правилом треугольника. Оно может быть также сформулировано и в другой форме: для любых трех точек А, В и С имеет место равенство  .
.
Для любых векторов  справедливы равенства:
справедливы равенства:
 (переместительный закон)
(переместительный закон)
 (сочетательный закон)
(сочетательный закон)
Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены. Вектором, противоположным нулевому вектору, считается нулевой вектор. Вектор  является противоположным вектору
является противоположным вектору  .
.
Сумма нескольких векторов не зависит от того, в каком порядке они складываются. Правило построения суммы нескольких векторов называется правилом многоугольника.
Разностью векторов 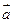 и
и  называется такой вектор, сумма которого с вектором
называется такой вектор, сумма которого с вектором  равна вектору
равна вектору 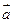 .
. 
Произведением ненулевого вектора 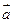 на число
на число  называется такой вектор
называется такой вектор  , длина которого равна
, длина которого равна  , причем векторы
, причем векторы 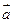 и
и  сонаправлены при
сонаправлены при  и противоположно направлены при
и противоположно направлены при  . Произведением нулевого вектора на любое число считается нулевой вектор. Произведение вектора
. Произведением нулевого вектора на любое число считается нулевой вектор. Произведение вектора 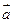 на число
на число  обозначается
обозначается  . Для любого числа
. Для любого числа  и любого вектора
и любого вектора 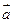 векторы
векторы 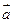 и
и  коллинеарны. Произведение любого вектора на число нуль есть нулевой вектор.
коллинеарны. Произведение любого вектора на число нуль есть нулевой вектор.
Для любых векторов  и любых чисел
и любых чисел  справедливы равенства:
справедливы равенства:
 (сочетательный закон)
(сочетательный закон)
 (первый распределительный закон)
(первый распределительный закон)
 (второй распределительный закон)
(второй распределительный закон)
Вектор  является вектором, противоположным вектору
является вектором, противоположным вектору 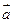 , т.е.
, т.е.  .
.
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Для сложения трех некомпланарных векторов используют правило параллелепипеда:


Примеры
Пример 1: Упростить выражения:
 Пример 2: Дан параллелепипед АВСМА1В1С1М1. Разложите вектор ВМ1 по векторам ВА, ВС и ВВ1.
Пример 2: Дан параллелепипед АВСМА1В1С1М1. Разложите вектор ВМ1 по векторам ВА, ВС и ВВ1.

Самостоятельная работа
1) Упростить выражения:

2) Дан тетраэдр АВСК.
1. Найти сумму векторов 
2. Доказать 
3) Дан параллелепипед АВСSА1В1С1S1. Назовите вектор, равный сумме векторов 
 2020-05-11
2020-05-11 231
231







