Теория
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление, которое обозначается стрелкой и выбрана единица измерения отрезков, то задана прямоугольная система координат в пространстве. Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Обычно она обозначается буквой О. Оси координат обозначаются Ох, Оу, Оz и называются ось абсцисс, ось ординат и ось аппликат. Вся система координат обозначается Охуz. В прямоугольной системе координат каждой точке М пространства ставится в соответствие тройка чисел, которые называются ее координатами.
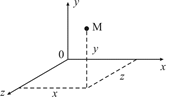
Пусть в пространстве задана прямоугольная система координат Охуz. На каждой из положительных полуосей от начала координат отложим единичный вектор – вектор, длина которого равна единице. Обозначим 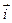 - единичный вектор оси абсцисс,
- единичный вектор оси абсцисс, 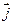 - единичный вектор оси ординат и
- единичный вектор оси ординат и 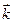 - единичный вектор оси аппликат. Векторы
- единичный вектор оси аппликат. Векторы 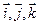 называются координатными векторами. Любой вектор
называются координатными векторами. Любой вектор 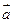 можно разложить по координатным векторам, т.е. представить в виде
можно разложить по координатным векторам, т.е. представить в виде 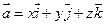 , причем коэффициенты разложения
, причем коэффициенты разложения 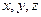 определяются единственным образом.
определяются единственным образом.
Коэффициенты 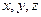 в разложении вектора
в разложении вектора 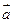 по координатным векторам называются координатами вектора
по координатным векторам называются координатами вектора 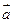 в данной системе координат. Координаты вектора
в данной системе координат. Координаты вектора 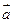 записываются в фигурных скобках после обозначения вектора:
записываются в фигурных скобках после обозначения вектора: 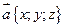 .
.
Координаты равных векторов соответственно равны, т.е. если векторы 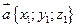 и
и 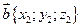 равны, то
равны, то 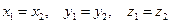 . Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Если 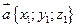 и
и 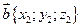 , то
, то 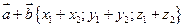
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если 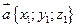 и
и 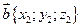 , то
, то 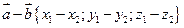 Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Если
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Если 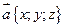 и
и 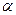 - данное число, то
- данное число, то 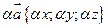
Если точка А имеет координаты 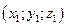 , а точка В имеет координаты
, а точка В имеет координаты 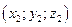 , то вектор АВ будет иметь координаты
, то вектор АВ будет иметь координаты  . Т.е. каждая координата вектора равна разности соответствующих координат его конца и начала.
. Т.е. каждая координата вектора равна разности соответствующих координат его конца и начала.
Примеры
Пример. Даны векторы 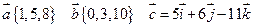 и точки
и точки 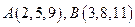 . Найти координаты векторов
. Найти координаты векторов 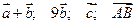
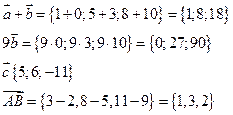
 2020-05-11
2020-05-11 370
370








