Самостоятельная работа

1) Даны векторы . Найти координаты векторов

2) Даны векторы  и точки . Найти координаты векторов

Тема: «Простейшие задачи в координатах»

Теория

Координаты середины отрезка

Если  и , М – середина отрезка АВ, то

Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

 

Длина вектора

Если известны координаты вектора 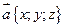, то длина этого вектора вычисляется по формуле

Расстояние между двумя точками

Расстояние между двумя точками  и  вычисляется по формуле

 

Примеры

Пример: Найти координаты точки М – середины отрезка АВ, если

Пример: Найти длину вектора

Пример: Найти расстояние между точками  и

Самостоятельная работа

1) Найти координаты точки М – середины отрезка АВ, если

2) Найти длины векторов , если

3) Найти координаты точки М – середины отрезка АВ, если

4) Найти длины векторов , если

Тема: «Скалярное произведение векторов»

Теория

Пусть угол между векторами  и  равен  (векторы  и  не сонаправлены). Если векторы  и  сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0°. Если угол между векторами равен 90°, то векторы называются перпендикулярными. Угол между векторами  и  обозначается .

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. Скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины. Скалярное произведение векторов  и  вычисляется по формуле

Свойства скалярного произведения:

1. , причем  при

2.  (переместительный закон)

3.  (распределит. закон)

4.  (сочетательный закон)

Косинус угла α между ненулевыми векторами  и  вычисляется по формуле  или

Примеры

Пример 1: Вычислить скалярное произведение векторов  , если

Пример 2: Найти угол между векторами  и