ТЕМА Простейшие тригонометрические уравнения
Вопросы темы:
Понятие простейшего тригонометрического уравнения и методом его решения с помощью тригонометрического круга.
2. Решение уравнений  и
и  .
.
Группа особых решений.
3. Решение уравнений 
Группа особых решений.
Цель занятия:
- Знакомство с понятием и видами простейших тригонометрических уравнений;
- Изучение метода решения простейших тригонометрических уравнений – с помощью тригонометрического круга;
- Закрепление знаний и понимания единичной окружности и тригонометрического круга.
Вопрос 1. Понятие простейшего
Тригонометрического уравнения
И методы его решения
Тригонометрическим уравнением называется равенство, в котором неизвестная величина (аргумент) находится под знаком тригонометрической функции.
Простейшими называются тригонометрические уравнения следующих четырёх видов:




Рассмотрим решение простейших тригонометрических уравнений, так как любое тригонометрическое уравнение различными методами и приемами в конечном счёте сводится к решению одного или нескольких простейших тригонометрических уравнений.
Задача решения простейшего тригонометрического уравнения – найти величину неизвестного угла х (аргумента).
Для решения простейшего тригонометрического уравнения используются:
- или тригонометрический круг,
- или график тригонометрической функции,
при четком знании и определении тригонометрических функций.
Рассмотрим решение простейших тригонометрических уравнений с помощью тригонометрического круга. Для этого рассмотрим следующие понятия и определения.
Тригонометрическим кругом называется система, состоящая из следующих числовых осей (см. ниже Рис.А):
● Единичная окружность – это окружность радиусом, равным единице, размещенная своим центром в центре прямоугольной системы координат ХОУ. Единичная окружность – это место расположения величин углов, выраженных в градусной или радианной системах измерения угла. Единичная окружность является числовой осью, деления которой являются значениями величин углов.
● Ось синусов, совпадающая с вертикальной осью ординат прямоугольной системы координат (ось ОУ) – место расположения значений синуса заданного угла. Так как единичная окружность имеет радиус, равным единице, то значения синуса заданного угла находятся в пределах от -1 до +1.
● Ось косинусов, совпадающая с горизонтальной осью абсцисс прямоугольной системы координат (ось ОХ) – место расположения значений косинуса заданного угла. Так как единичная окружность имеет радиус, равным единице, то значения синуса заданного угла находятся в пределах от -1 до +1.
● Ось тангенсов – это линия, параллельная вертикальной оси ОУ и проведенная как касательная к точке пересечения линии единичной окружности с осью ОХ в точке +1, является местом расположения значений тангенса заданного угла. Значения тангенса угла изменяются в пределах от -∞ до +∞.
● Ось котангенсов – это линия, параллельная горизонтальной оси ОХ и проведенная как касательная к точке пересечения линии единичной окружности с осью ОУ в точке +1, является местом расположения значений котангенса заданного угла. Значения котангенса угла изменяются в пределах от -∞ до +∞.

Рис.А
Используя для решений простейших тригонометрических уравнений тригонометрический круг, на его числовых осях будем отмечать деления с уже изученными нами ранее (представлены на Рис. А):
- табличными значениями углов (в градусах или радианах) – на единичной окружности;
- табличными значениями синусов заданных углов – на оси синусов (ось ОУ);
- табличными значениями косинусов заданных углов – на оси косинусов (ось ОХ);
- табличными значениями тангенсов заданных углов – на оси тангенсов (вертикальная ось, параллельная оси ОУ);
- табличными значениями котангенсов заданных углов – на оси котангенсов (горизонтальная ось, параллельная оси ОХ).
Наша задача – рассмотреть решение простейших тригонометрических уравнений вида:
 ,
,  ,
, 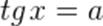 ,
,  .
.
Из известных нам табличных значений углов и табличных значений тригонометрических функций выделим две группы решений простейших тригонометрических уравнений, в зависимости от величины а, где а – это известное нам значение тригонометрической функции:
- группа 1 – особые решения – если а = 0, +1, -1.
- группа 2 – другие «табличные решения»:
для синуса и косинуса – если а = +½; -½; +√2/2; -√2/2; +√3/2; -√3/2;
для тангенса и котангенса – если а = +1/√3; -1/√3; +√3; -√3.
Порядок решения простейшего тригонометрического уравнения
В простейшем тригонометрическом уравнении вида
 ,
,  ,
, 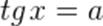 ,
, 
нам известны:
- функция (sin, сos, tg или ctg);
- значение этой функции, то есть а;
нам не известно:
- значение угла (аргумента) х.
Поэтому задачей решения простейшего тригонометрического уравнения является определение неизвестного угла х, если нам известно значение (а) соответствующей тригонометрической функции этого угла.
Главная идея решения простейшего тригонометрического уравнения с помощью тригонометрического круга заключается в следующих действиях:
1. Нарисовать единичную окружность.
2. Вынести на соответствующую числовую ось (ось синусов, косинусов, тангенсов или котангенсов) положение заданного (известного нам) числа а.
3. Определить на единичной окружности значение величины угла (найти точку х на единичной окружности), синус, косинус, тангенс, контангенс которого дает нам заданное (известное нам) число а.
Для синуса и косинуса – это перпендикуляр, опущенный из точки х на единичной окружности на соответствующую числовую ось (sin или cos), смотри пояснения ниже на Рис. Б.
Для тангенса и котангенса – это точка пересечения продолжения луча угла х с соответствующей числовой осью (tg или ctg) (см. ниже Рис. В, Рис. Г).
Чтобы эта идея проявилась наиболее отчётливо, необходимо рассмотреть решения уравнений группы 1 и группы 2, когда в правой части уравнений будут стоять табличные значения тригонометрических функций (а).
 2020-05-11
2020-05-11 598
598







