Группа Особых решений

Вспомним, что:

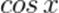-  — это абсцисса точки х, расположенной на единичной окружности и соответствующей углу х. Чтобы найти абсциссу точки х, расположенной на единичной окружности, опускаем перпендикуляр из этой точки на ось косинусов (ось ОХ – ось абсцисс) (Рис.Б).

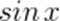-  — это ордината точки х, расположенной на единичной окружности и соответствующей углу х. Чтобы найти ординату точки х, расположенной на единичной окружности, опускаем перпендикуляр из этой точки на ось синусов (ось ОУ – ось ординат) (Р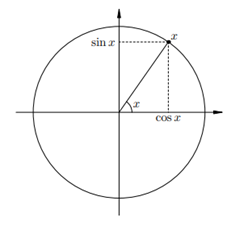ис.Б).

Рис.Б

Дополним, что из определения синуса и косинуса следует, что уравнения 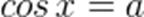    и 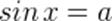   имеют решения только при условии .

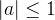Поэтому необходимо помнить, что, например, уравнения, подобные представленным: sinx = 3/2 или   cosx = 7 решений не имеют!

 

Рассмотрим группу 1 Особых решений – для значений тригонометрических функций синус и косинус, равных +1, -1 или 0.

. .

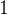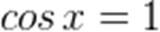Идя по алгоритму решения простейшего тригонометрического уравнения:

- представим схему единичной окружности (Рис.1);

- отметим на оси косинусов (ось ОХ) заданное значение величины cosx, равное 1 (а = 1) – это точка пересечения единичной окружности с осью ОХ;

- обращаем внимание, что на единичной окружности имеется лишь одна точка, которая при проведении перпендикуляра от этой точки на ось косинусов (ось ОХ) даст абсциссу, равную 1. Эта точка равна значению на единичной окружности 0 радиан (см.р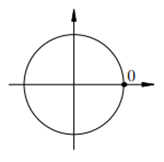ис.1):

Рис.1

Эта точка, равная 0 радиан, и есть решение данного простейшего тригонометрического уравнения.

Далее, при совершении бесконечного числа целых оборотов (2π), получим бесконечное множество таких точек на единичной окружности, абсциссы которых равны 1.

Следовательно, будем иметь целую серию решений (значений х): 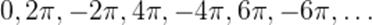, косинус которых равен 1.

Все эти углы получаем из нулевого угла прибавлением целого числа полных оборотов 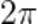, то есть, целое число полных оборотов как в одну сторону (против часовой стрелки), так и в другую сторону (по часовой стрелке).

Это множество решений данного уравнения можем записать в общем виде (для любого числа оборотов, то есть для любого числа n) одной формулой:

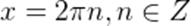
где n – число оборотов, выраженное положительным или отрицательным целым числом из множества целых чисел Z.

 

. .

 

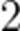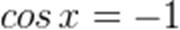Идя по алгоритму решения простейшего тригонометрического уравнения:

- представим схему единичной окружности (Рис.2);

- отметим на оси косинусов (ось ОХ) заданное значение величины cosx, равное - 1 (а = -1) – это точка пересечения единичной окружности с осью ОХ в левой, отрицательной, части числовой оси;

- обращаем внимание, что на единичной окружности имеется лишь одна точка, которая при проведении перпендикуляра от этой точки на ось косинусов (ось ОХ) даст абсциссу, равную - 1. Эта точка равна значению на единичной окружности π радиан (см.р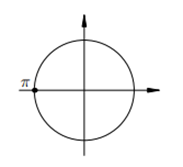ис.2):

Рис.2

Эта точка, равная π радиан, и есть решение данного простейшего тригонометрического уравнения.

 

Далее, при совершении бесконечного числа целых оборотов (2 π), получим бесконечное множество таких точек на единичной окружности, абсциссы которых равны - 1.

Следовательно, будем иметь целую серию решений (значений х): π, -π, 3π, -3π, 5π, -5π, …,, косинус которых равен - 1.

Все множество решений данного уравнения можем записать в общем виде (для любого числа оборотов, то есть для любого числа n) одной формулой:

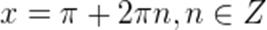
где n – число оборотов, выраженное положительным или отрицательным целым числом из множества целых чисел Z.

 

. .

 

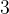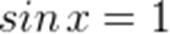Идя по алгоритму решения простейшего тригонометрического уравнения:

- представим схему единичной окружности (Рис.3);

- отметим на оси синусов (ось ОУ) заданное значение величины sinx, равное 1 (а = 1) – это точка пересечения единичной окружности с осью ОY;

- обращаем внимание, что на единичной окружности можем выделить только одну точку, которая при проведении перпендикуляра от этой точки на ось синусов (ось ОУ) даст ординату, равную 1. Эта точка на единичной окружности соответствует значению угла, равного π/2 радиан (см.р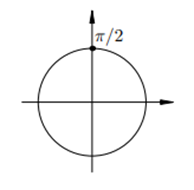ис.3):

Рис.3

Эта точка на единичной окружности, равная π/2 радиан, и есть решение данного простейшего тригонометрического уравнения.

Далее, при совершении бесконечного целого числа поворотов (2π) против часовой стрелки и по часовой стрелке, получим целую серию решений (множество значений х), при которых sinx будет равен 1, это значения х: π/2; π/2±2π; π/2±4π; π/2±6π;…

 

Это множество решений (для любого числа оборотов, то есть для любого числа n) можем записать одной формулой, решением в общем виде

 

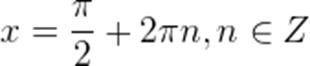
где n – число оборотов, выраженное положительным или отрицательным целым числом из множества целых чисел Z.

 

. .

 

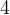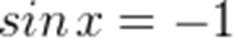Идя по алгоритму решения простейшего тригонометрического уравнения:

- представим схему единичной окружности (Рис.4);

- отметим на оси синусов (ось ОУ) заданное значение величины sinx, равное - 1 (а = - 1) – это точка пересечения единичной окружности с осью ОY в нижней, отрицательной, части числовой оси ОУ;

- обращаем внимание, что на единичной окружности можем выделить только одну точку, которая при проведении перпендикуляра от этой точки на ось синусов (ось ОУ) даст ординату, равную - 1. Эта точка на единичной окружности соответствует значению угла, равного - π/2 радиан (см.р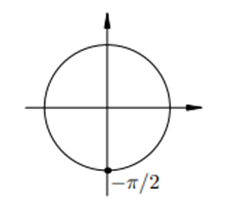ис.4):

Рис.4

Эта точка на единичной окружности соответствует значению угла, равного - π/2 радиан (если отметим точку на единичной окружности, идя по часовой стрелке) и 3π/2 радиан (если пойдем против часовой стрелки).

Принято за решение принимать первый вариант: - π/2 радиан.

 

 

Далее при совершении бесконечного целого числа поворотов (2π) против часовой стрелки и по часовой стрелке получим целую серию решений (множество значений х), при которых sinx будет равен - 1, это значения х: -π/2; -π/2±2π; -π/2±4π; -π/2±6π;…

 

Это множество решений (для любого числа оборотов, то есть любого числа n) можем записать одной формулой, решением в общем виде

 

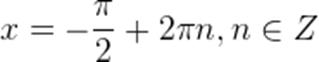
где n – число оборотов, выраженное положительным или отрицательным целым числом из множества целых чисел Z.

 

. .

 

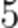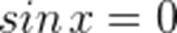Идя по алгоритму решения простейшего тригонометрического уравнения:

- представим схему единичной окружности (Рис.5);

- отметим на оси синусов (ось ОУ) заданное значение величины sinx, равное 0 (а = 0), где sinx равен нулю – это точки пересечения единичной окружности с осью ОХ в правой и левой частях числовой оси ОХ;

- обращаем внимание, что на единичной окружности можем выделить две точки, которые при проведении перпендикуляра от этих точек на ось синусов (ось ОУ) имеют ординату, равную 0. Это две точки на единичной окружности, которые соответствуют значениям углов, равных 0 и π радиан (см.р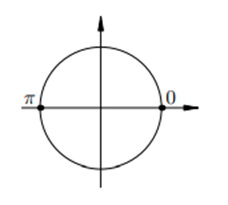ис.5):

Рис.5

Эти две точки на единичной окружности, равные 0 и π радиан, и есть решения данного простейшего тригонометрического уравнения.

Далее при совершении бесконечного целого числа поворотов (π) против часовой стрелки и по часовой стрелке получим целую серию решений (множество значений х), при которых sinx будет равен 0, это значения х: 0; ±π; ±2π; ±3π;…

Все эти углы получаем из нулевого угла прибавлением целого числа углов 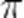 (то есть с помощью нескольких полуоборотов в обе стороны).

Таким образом можем записать это множество решений данного уравнения одной формулой, решение в общем виде (для любого числа оборотов, то есть для любого числа n):

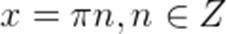
где n – число оборотов, выраженное положительным или отрицательным целым числом из множества целых чисел Z.

Точки, лежащие на концах диаметра тригонометрического круга, называем диаметральной парой, в данном случае, горизонтальной.

. .

 

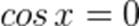Идя по алгоритму решения простейшего тригонометрического уравнения:

- представим схему единичной окружности (Рис.6);

- отметим на оси косинусов (ось ОХ) заданное значение величины cosx, равное 0 (а = 0), где cosx равен нулю – это точки пересечения единичной окружности с осью ОУ в положительной и отрицательной частях числовой оси ОУ;

- обращаем внимание, что на единичной окружности можем выделить две точки, которые при проведении перпендикуляра от этих точек на ось косинусов (ось ОХ) имеют абсциссу, равную 0. Это две точки на единичной окружности, которые соответствуют значениям углов, равных π/2 и 3 π/2 радиан (см.р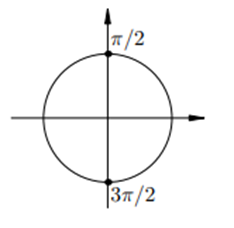ис.6):

Рис.6

Эти две точки на единичной окружности, равные π/2 и 3 π/2 радиан, и есть решения данного простейшего тригонометрического уравнения. При этом второе решение х = 3 π/2  получим путем полуоборота (π) от угла, равного радиан.

Поэтому, далее при совершении бесконечного целого числа поворотов (π) (полуоборотов) против часовой стрелки и по часовой стрелке получим целую серию решений (множество значений х), при которых cosx будет равен 0, это значения х: ±π/2; ±3π/2; ±5π/2;…

Все эти углы получаем из первого угла π/2 путем прибавления целого числа полуповоротов π (то есть с помощью нескольких полуоборотов в обе стороны).

Таким образом можем записать полученную серию решений данного уравнения одной формулой, решение в общем виде (для любого числа оборотов, то есть для любого числа n):

 

.

 

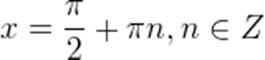где n – число оборотов, выраженное положительным или отрицательным целым числом из множества целых чисел Z.

 

Точки, лежащие на концах диаметра тригонометрического круга, называем диаметральной парой, в данном случае – вертикальной.