Расчёт равновесия жидкости в движущихся сосудах

    При движении сосуда в горизонтальном направлении с постоянным ускорением (замедлением) на жидкость, находящуюся в нём, действует сила тяжести и сила инерции. Свободная поверхность представляет собой наклонную плоскость, уравнение которой имеет вид

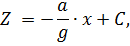
где  C – постоянная величина; a – ускорение сосуда.

    Гидростатическое давление в любой точке жидкости

где   h – расстояние по вертикали от точки до свободной поверхности.

    Сила давления на плоскую стенку в этом случае

) ,

где  и  - расстояния по вертикали от центра тяжести стенки до свободной поверхности жидкости и до пьезометрической плоскости соответственно.

Пример расчёта.

    В кузов автомобиля – самосвала до уровня 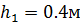 налит цементный раствор, плотностью 𝜌=2200 кг/м³. Определить наименьший допустимый путь торможения самосвала от скорости υ =36 км/ч до остановки исходя из условия, чтобы раствор не выплеснулся из кузова. Определить силу давления раствора на передний борт при торможении. Для упрощения принять, что кузов самосвала имеет форму прямоугольной коробки размерами ℓ =2,5 м; h=0,8 м; ширина кузова b =1,8 м, а движение автомобиля прямолинейное, равнозамедленное.

Рисунок 3 Схема смещения груза при торможении.

Дано:

υ =36 км/ч; ℓ =2,5 м; h=0,8 м;: b =1,8 м;

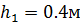; 𝜌=2200 кг/м³.

Решение:

    На раствор в кузове действуют две силы: тяжести G, направленная вниз и инерции F = m·𝛼, направленная вправо при торможении автомобиля. Решая дифференциальное уравнение поверхности уровня получаем, при X= 𝛼, Y=0,

Z= - g.

,

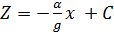    Где  =  –тангенс угла наклона свободной поверхности жидкости к горизонту, значение которого в условиях данной задачи равно

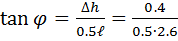= 0.31

    Следовательно замедление автомобиля 𝛼 = ∙g

𝛼 = 9.81·0.31=3.02м/с² .

    Длину торможения автомобиля найдём из уравнений равнозамедленного движения

, где  .

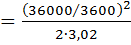
   Определим силу давления раствора на передний борт автомобиля

  S;

F =  ∙1.8∙0.8 =1.24∙ 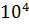Н.