Лекция: свойства графов
Маршруты, цепи, циклы.
Определение 1. а) Чередующаяся последовательность вершин и ребер графа G (неориентированного), начинающаяся и завершающаяся вершинами, называется маршрутом, который называется циклическим, если его начальная и конечная вершины совпадают. Длина маршрута – число встречающихся в нем ребер.
б) Маршрут называется цепью, а циклический маршрут – циклом, если каждое его ребро встречается в нем не более одного раза (вершины в цепи и цикле могут повторяться и несколько раз).
г) Цепи и циклы называются простыми, если в них никакие вершины не повторяются.
е) Цепь называется подвешенной, если из всех ее вершин только первая и последняя лежат не менее чем на трех ребрах графа G.
Компонентой графа называется его подграф, каждые две вершина которого можно соединить цепью.
Определение 2. Число компонент графа G обозначается 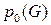 (в терминах алгебраической топологии оно называется числом Бетти размерности нуль графа G).
(в терминах алгебраической топологии оно называется числом Бетти размерности нуль графа G).
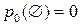 .
. 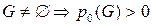 .
.
Определение 3. Если 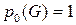 , то граф G называется связным, если же
, то граф G называется связным, если же 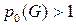 , то G называется несвязным графом.
, то G называется несвязным графом.
Число 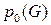 характеризует структурные свойства G. Из Определения 2 следует, что только нуль-граф ни связен, ни несвязен, а для G, не имеющего ребер
характеризует структурные свойства G. Из Определения 2 следует, что только нуль-граф ни связен, ни несвязен, а для G, не имеющего ребер 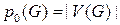 , а каждая компонента G является связным графом.
, а каждая компонента G является связным графом.
Цикломатическое число и его свойства.
Определение 1. Цикломатическое число 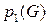 графа G определяется формулой
графа G определяется формулой
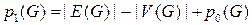 .
.
Оно является второй структурной характеристикой графа G и также называется числом Бетти размерности 1, а число 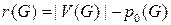 – рангом графа G. Цикломатическое число
– рангом графа G. Цикломатическое число 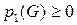 , так как справедлива простая
, так как справедлива простая
Теорема 1. Пусть мультиграф 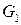 получен из мультиграфа G добавлением нового ребра между
получен из мультиграфа G добавлением нового ребра между 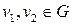 . Если
. Если  или
или 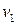 и
и 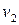 могут быть соединены цепью в G, то
могут быть соединены цепью в G, то 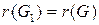 и
и 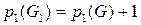 , иначе,
, иначе, 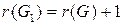 и
и 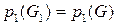 .
.
Отождествим каждый цикл m мультиграфа G с вектором 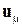 . Для этого придадим каждому ребру G произвольную ориентацию и положим, что при прохождении цикла m через ребро
. Для этого придадим каждому ребру G произвольную ориентацию и положим, что при прохождении цикла m через ребро 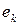 в направлении его ориентации координата вектора
в направлении его ориентации координата вектора 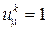 , а в противоположном направлении
, а в противоположном направлении 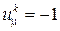 .
.
Полученный таким образом вектор 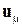 размерности
размерности 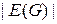 называется вектором-циклом, соответствующим циклу m. Циклы называются независимыми, если соответствующие им векторы линейно независимы (это свойство не зависит от выбора ориентации ребер).
называется вектором-циклом, соответствующим циклу m. Циклы называются независимыми, если соответствующие им векторы линейно независимы (это свойство не зависит от выбора ориентации ребер).
Справедлива
Теорема 2. Цикломатическое число 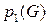 мультиграфа G равно наибольшему числу независимых циклов.
мультиграфа G равно наибольшему числу независимых циклов.
Определение 2. Максимальное множество независимых циклов графа G называется базой соответствующего векторного пространства, причем его размерность совпадает с цикломатическим числом 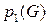 .
.
 2020-05-21
2020-05-21 182
182







