Приведем другое решение пункта а)

Пусть окружность касается оснований BC и AD в точках K и L соответственно, ее центр находится в точке O, а BM = x, CN = y, тогда AM = 8 x, DN = 2 y. Поскольку точки M, K, N и L — точки касания, , , 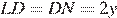и Опустим высоты BH и CQ:

тогда по теореме Пифагора Поскольку имеем откуда

Таким образом, BC = BK + KC = 3 x, AD = AL + LD = 12 x, то есть AD = 4 BC.

17. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

− каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.

Если ежегодно выплачивать по 58 564 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рублей, то кредит будет полностью погашен за 2 года. Найдите r.

Решение.

Пусть сумма кредита S ежегодные выплаты x, По условию долг на июль меняется так:

Если долг выплачен двумя равными платежами x ₂, то откуда

Если долг выплачен четырьмя равными платежами x ₄, то откуда

Тогда

откуда Следовательно,

Ответ: 10.

18. При каких значениях параметра а система 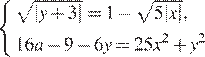имеет четыре решения?

Решение.

Полагая , перепишем исходную систему в виде

Заметим, что если хотя бы одна из переменных отрицательна, то исходная система не имеет решений. Значению соответствует , а значению соответствует а каждой паре положительных значений соответствует по два значения исходных переменных соответственно, то есть каждому такому решению соответствуют четыре решения исходной системы.

Заметим далее, что если пара является решением системы, то и пара — также решение этой системы, то есть исходная система получает восемь решений если Таким образом, исходная система имеет четыре решения тогда и только тогда, когда полученная система имеет следующие решения: или , где и

Рассмотрим три случая.

1. Если то из первого уравнения из второго уравнения 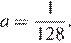При найденном значении параметра система принимает вид

Осталось убедиться, что данная система не имеет других решений, кроме Из первого уравнения подставим во второе:

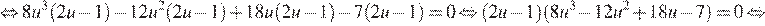
Последнее уравнение имеет единственный корень Это доказывает, что других решений система не имеет.

2. Если а то 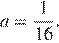При этом значении параметра система принимает вид

Проверим, имеет ли данная система решения, отличные от . Из первого уравнения снова подставим во второе:

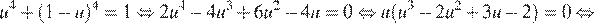
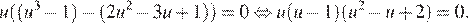
Последнее уравнение имеет два корня и Первый из них соответствует рассматриваемому случаю и двум решениям исходной системы, а второй оставшемуся случаю и еще двум.

3. Если а то 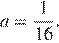Как было показано выше, данное значение параметра является искомым.

Ответ:

19. Три числа назовем хорошей тройкой, если они могут быть длинами сторон треугольника.

Три числа назовем отличной тройкой, если они могут быть длинами сторон прямоугольного треугольника.

а) Даны 8 различных натуральных чисел. Может ли оказаться. что среди них не найдется ни одной хорошей тройки?

б) Даны 4 различных натуральных числа. Может ли оказаться, что среди них можно найти три отличных тройки?

в) Даны 12 различных чисел (необязательно натуральных). Какое наибольшее количество отличных троек могло оказаться среди них?

Решение.

а) Если числа равны 1, 2, 4, 8, 16, 32, 64 и 128, то никакие три из них не образуют хорошую тройку.

Другой пример — последовательность чисел Фибоначчи без первой единицы: 1, 2, 3, 5, 8, 13, 21, 34.

б) Если одно из чисел является длиной гипотенузы для двух треугольников, какое-то из оставшихся трёх чисел является длиной катета для этих двух треугольников, а тогда треугольники окажутся равными по гипотенузе и катету. Значит, каждое число может быть длиной гипотенузы не более чем одного треугольника. При этом два самых маленьких числа не могут являться длиной гипотенузы треугольника. Значит, среди четырёх чисел можно найти не более двух отличных троек.

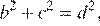
Другое рассуждение для п. б). Расположим числа в порядке возрастания: и отметим, что гипотенузой могут быть только два больших числа. Запишем три равенства на гипотенузу треугольника: и заметим, что из последних двух равенств следует равенство чисел противоречащее условию.

в) Упорядочим числа по возрастанию. Самое большое из них может быть длиной гипотенузы не более чем в пяти треугольниках (в противном случае одно из оставшихся 11 чисел будет длиной катета в двух треугольниках с данной гипотенузой, а тогда эти треугольники будут равны по гипотенузе и катету). Аналогично, второе по величине число может быть длиной гипотенузы не более чем в пяти треугольниках, третье и четвёртое — в четырёх, пятое и шестое — в трёх. седьмое и восьмое — в двух, девятое и десятое — в одном. Итого. отличных троек может получиться не более 30. Тридцать отличных троек найдётся, например, для следующего набора чисел:

Ответ: а) да; б) нет; в) 30.

Примечание.

Заметим, что при решении пункта б) не требуется, чтобы числа были натуральными, ни даже целыми. Никакие четыре различных числа не могут дать три пифагоровы тройки.

С другой стороны, отметим, что четыре различных натуральных числа могут образовать одну пифагорову тройку, но не могут образовать двух пифагоровых троек. В теории чисел этот факт известен как одна из эквивалентных формулировок теоремы Ферма о прямоугольном треугольнике: не существует двух пифагоровых троек, в которых два катета одной тройки являются катетом и гипотенузой другой тройки. Доказательство этого факта было дано самим Ферма и может быть исследовано читателем самостоятельно.

Вариант № База.

1. Найдите значение выражения .

Решение.

Умножим числитель и знаменатель на 10 000:

Ответ: 10.

2. Найдите значение выражения .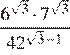

Решение.

Выполним преобразования:

Ответ: 42.

3. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?

Решение.

Цена чайника после повышения стала составлять 116% от начальной цены. Разделим 3480 на 1,16:

Значит, цена чайника до повышения составляла 3000 рублей.

Ответ: 3000.

4. Теорему косинусов можно записать в виде где a, b и c — стороны треугольника, а γ — угол между сторонами a и b. Пользуясь этой формулой, найдите величину cos γ, если a = 7, b =10 и c = 11.

Решение.

Подставим переменные в формулу:

Ответ: 0,2.

5. Найдите , если .

Решение.

Выполним преобразования:

Ответ: 10.

6. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

Решение.

Больному нужно выпить 0,5 · 3 · 21 = 31,5 г лекарства. В одной упаковке содержится 0,5 · 10 = 5 г лекарства. Разделим 31,5 на 5:

Значит, на курс лечения необходимо 7 упаковок.

Ответ: 7.

7. Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Решение.

На ОДЗ перейдем к уравнению на основание логарифма:

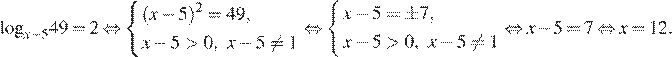
Ответ: 12.

Примечание.

Область определения уравнения состоит из чисел, больших 1 и отличных от 2. Поэтому число −2, которое некоторые ошибочно считают меньшим корнем уравнения, не является его решением.

8. Садовод решил разбить на своём дачном участке 4 квадратные клумбы и 8 клумб в виде правильных треугольников, огородив каждую из них небольшим заборчиком. Длина каждой стороны у любой клумбы равна одному метру. Найдите общую длину всех заборчиков в метрах.

Решение.

Длина всех заборчиков равна периметру четырех квадратов и восьми правильных треугольников. Периметр квадрата со стороной 1 равен четырем, а значит периметр четырех квадратов равен 16. Периметр правильного треугольника со стороной 1 равен 3, а значит периметр восьми правильных треугольников равен 3 · 8=24.

Длина заборчиков 24+16=40.

Ответ: 40.

9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

ВЕЛИЧИНЫ		ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) площадь одной страницы учебника Б) площадь территории республики Карелия В) площадь одной стороны монеты Г) площадь бадминтонной площадки		1) 81,7 кв. м 2) 330 кв. см 3) 180,5 тыс. кв. км 4) 300 кв. мм

В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.

A	Б	В	Г

Решение.

Площадь республики Карелия огромна и вполне может быть 180,5 тыс. кв. км., площадь бадминтонной площадки около 81,7 кв. м., площадь страницы учебника ориентировочно 330 кв. см., а площадь монеты на глаз около 300 кв. мм. Получим соответствие Б - 3, Г - 1, А - 2 и В - 4. Окончательно получим 2341.

Ответ: 2341.

10. В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

Решение.

Пусть один из близнецов находится в некоторой группе. Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников. Вероятность того, что второй близнец окажется среди этих 12 человек, равна 12: 25 = 0,48.

11. На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали — цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько рабочих дней из данного периода цена золота была между 970 и 980 рублями за грамм.

Решение.

Из графика видно, что из данного периода цена золота была между 970 и 980 рублями за грамм 7 дней (см. рисунок).

Ответ: 7.

12. В трёх салонах сотовой связи один и тот же смартфон продаётся в кредит на разных условиях. Условия приведены в таблице.

Салон	Стоимость смартфона (руб.)	Первоначальный взнос (в % от стоимости)	Срок кредита (мес.)	Сумма ежемесячного платежа (руб.)
Эпсилон	11 000	25	12	940
Дельта	12 400	30	12	880
Омикрон	13 400	20	6	1900

Определите, в каком из салонов покупка обойдётся дешевле всего (с учётом переплаты). В ответе запишите стоимость этой покупки в рублях.

Решение.

Рассчитаем стоимость покупки с доставкой в трёх салонах связи:

Эпсилон: 11 000 · 0,25 + 940 · 12 = 14 030.

Дельта: 12 400 · 0,3 + 880 · 12 = 14 280.

Омикрон: 13 400 · 0,2 + 1900 · 6 = 14 080.

Ответ: 14 030.

13. В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Для того чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.

Решение.

Объем вытесненной жидкости равен объему детали (закон Архимеда). Уровень жидкости поднялся на h=20 см, сторона основания a=20 см, значит, вытесненный объем будет равен Найденный объём является объёмом детали.

Ответ: 8000.

14. На рисунке изображён график функции , к которому проведены касательные в четырёх точках.

Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной.

ТОЧКИ		ЗНАЧЕНИЕ ПРОИЗВОДНОЙ
А) A Б) B В) C Г) D		1) −4 2) 0,2 3) −0,2 4) 1,5

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

A	Б	В	Г

Решение.

Пусть угол, который составляет касательная с положительным направлением оси абсцисс, равен α, а угловой коэффициент касательной равен k. Тогда:

α	k

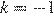
Значение производной в точке равно угловому коэффициенту касательной, проведённой в этой точке. Таким образом, получаем соответствие: А — 4, Б — 3, В — 1 и Г — 2.

Ответ: 4312.

15. Найдите квадрат длины вектора .

Решение.

Длина вектора определяется следующим выражением:

Поэтому

Ответ: 40.

16. В правильной четырехугольной пирамиде высота равна 8, боковое ребро равно 10. Найдите ее объем.

Решение.

В основании правильной четырехугольной пирамиды лежит квадрат. Пусть его центр — точка О, по теореме Пифагора находим тогда длина диагонали основания равна 12. Площадь квадрата равна половине произведения его диагоналей, поэтому она равна 72. Следовательно, для объема пирамиды имеем:

Ответ: 192.

17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

НЕРАВЕНСТВА		РЕШЕНИЯ
А) Б) В) Г)		1) 2) 3) 4)

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А	Б	В	Г

Решение.

А)

Б)

В)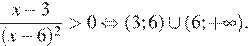

Г)

Ответ: 2413.

18. В офисе фирмы компьютеры работают только от сетевого электропитания. Если компьютеры работают, то электричество в офисе есть. Выберите утверждения, которые непосредственно следуют из этих данных.

1) Если в офисе нет электричества, то компьютеры не работают.

2) Если в офисе есть электричество, то компьютеры работают.

3) Если компьютеры не работают, значит, в офисе нет электричества.

4) Если в офисе нет электричества, то не работает компьютер директора.

В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Решение.

1) Это так, поскольку компьютеры работают только от сетевого электропитания.

2) Необязательно. Возможно, что электричество есть, но компьютеры никто не включал.

3) Как и в прошлом пункте, наличие электричества ничего не говорит о работе компьютеров. Они могут как работать, так и не работать.

4) Если в офисе нет электричества, то ни один компьютер не работает, включая компьютер директора.

Ответ: 14.

19. Сумма цифр трёхзначного числа A делится на 13. Сумма цифр числа A +5 также делится на 13. Найдите такое число A.

Решение.

Пусть число имеет вид Если , то сумма цифр в новом числе будет на 5 больше, чем в исходном. Пусть делится на 13, тогда то есть число не делится на 13. Аналогично, если число делится на 13, то число не делится на 13. Значит, . Рассмотрим 3 случая:

1) Число имеет вид: , сумма цифр числа на 3 меньше суммы цифр числа

2) Число имеет вид: , сумма цифр числа 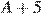на 12 меньше суммы цифр числа

3) Число имеет вид: , сумма цифр числа на 21 меньше суммы цифр числа

Ясно, что условиям задачи удовлетворяют числа, рассмотренные в пункте 2). Подберём число так, чтобы сумма его цифр делилась на 13. Наименьшее возможное удовлетворяющее условиям задачи, — 899.

Ответ: 899.

20. В обменном пункте можно совершить одну из двух операций:

• за 2 золотых монеты получить 3 серебряных и одну медную;

• за 5 серебряных монет получить 3 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?

Решение.

Пусть Николай сделал сначала операций второго типа, а затем операций первого типа. Тогда имеем: