Задача Эйлера про мосты

Мы уже много раз говорили про то, что решение любой практической задачи начинается с построения математической модели.

Но иногда модель сводится к эквивалентной математической задаче, которая оказывается важнейшим инструментом для решения целого класса других, совершенно непохожих, на первый взгляд, задач. Одним из таких примеров является задача Эйлера про мосты.

Издавна среди жителей Кенигсберга (сейчас – Калининграда) была распространена такая загадка: как пройти по всем городским мостам (через реку Преголя), не проходя ни по одному из них дважды (см. рис. 11)?

Рис. 5. Иллюстрация к задаче Эйлера про мосты

В задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера (см. рис. 12). Он доказал, что сделать это нельзя.

Рис. 6. Леонард Эйлер

Но важно, конечно, не само решение этой шуточной задачи, а то, что, решая ее, Эйлер свел ее к эквивалентной формулировке, которая помогла разработать принципиально новый математический инструмент – теорию графов, которая сейчас повсеместно используется, например в программировании.

Основная идея Эйлера: нам не важны размеры мостов, значит, их можно считать линиями, а также размеры частей города – их можно считать точками (см. рис. 13). Тогда задача сводится к такой: можно ли нарисовать такой граф, не отрывая карандаша от бумаги.

Рис. 7. Мосты можно считать линиями, а города – точками, т. к. их размеры не важны

Решая задачу про мостов, Эйлер вывел несколько важных теорем, касающихся различных графов. Одна из них говорила, что граф с более чем двумя нечетными вершинами (т. е. вершинами, к которым ведет нечетное число ребер) нельзя начертить одним росчерком.

Интуитивное доказательство этого утверждения несложное: рисуя граф, не отрывая руки, мы должны входить и выходить из каждой точки одинаковое количество раз, т. е. в точке должно сходиться только четное количество ребер (см. рис. 14).

Рис. 8. Чтобы граф можно было нарисовать, не отрывая руки, у него должно быть не более двух нечетных вершин

Исключение составляют две вершины – начало (из этой точки мы выходим на один раз больше, чем входим) и конец (для него все наоборот). Если же таких вершин больше, то начертить граф одним росчерком не получится. У графа из задачи про мостов все вершины нечетные (см. рис. 15), поэтому задача не имеет решения.

Рис. 9. У графа из задачи про мостов все вершины нечетные

Для нас важнее отметить, что правильная эквивалентная формулировка условия и упрощение модели – залог решения любой задачи.

Факториал

Если пронумеровать места в машине, то объяснение выйдет намного короче: на первое место 4 варианта выбора, на второе – 3, на третье – 2, на четвертое – 1:

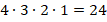
Интересно, что такое решение подойдет к множеству подобных задач: «сколько четырехзначных чисел можно составить из цифр , если каждую цифру можно использовать ровно 1 раз» или «сколькими способами можно переставить буквы в слове «парк»» и т. д.

Подобные задачи называются «задачами на перестановки», ведь в них мы, по сути, считаем количество вариантов переставить некоторые различные элементы. Только что мы рассчитали количество перестановок четырех элементов (см. рис. 16):

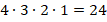
Рис. 16. Количество перестановок четырех элементов

В общем случае, если у нас будет элементов, то, применяя правило умножения, мы получим: (и т. д. до ). Сокращенно это произведение обозначают и записывают так (а называют «эн факториал»):

 

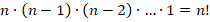
Повторения в задачах на перестановки

Рассчитывая количество вариантов, используя правила умножения и сложения, нужно быть внимательным. Иногда возникают такие ситуации, когда один и тот же вариант мы считаем по несколько раз.

Например, как мы уже знаем, в слове «парк» можно переставить буквы 24 различными способами. Попробуем сделать то же самое со словом «пара».

Обратите внимание, что у нас есть одинаковые буквы. Получив ответ 24, мы посчитали каждую из них по 2 раза (см. рис. 17). На самом деле, различных перестановок будет ровно в 2 раза меньше – 12 (см. рис. 18).

Рис. 17. Количество перестановок букв в слове «пара» с повторениями

Рис. 18. Количество перестановок букв в слове «пара» без повторений

Почему так вышло? Подсчитывая перестановки, мы считали первую букву «а» и вторую букву «а» различными. Но это одна и та же буква и, переставляя их между собой местами, мы не получим нового слова. Именно поэтому, мы делим на 2 – это количество перестановок 2 элементов: .

Кроме повторений при подсчете вариантов, вы можете встретиться с такой ситуацией, когда нельзя однозначно определить количество вариантов при выборе. Например, количество перестановок в слове «пара» мы можем попробовать посчитать по-другому.

Первую букву можно выбрать 3 способами (п, р, а), вторую букву…, а вот тут и непонятно: если мы выбрали первой букву «а», то у нас по-прежнему 3 варианта («п, р, а»). Если «п» или «р», то останется только 2 варианта («а, р» и «а, п» соответственно). В таком случае придется рассмотреть отдельно эти варианты. Чтобы не запутаться в них, лучше изобразить выбор графически (см. рис. 19).

Рис. 19. Количество перестановок в слове «пара»

Получим:

Более подробно такие задачи мы разберем во время практического занятия.

Перестановки, размещения, сочетания

Большинство комбинаторных задач сводятся к одному из четырех классических типов.

1. С одним из них мы уже познакомились – это расчет количества перестановок различных элементов (см. рис. 20). Число перестановок элементов принято обозначать («пэ из эн»). Значение этой величины мы уже вычислили:

Рис. 20. Перестановка элементов

2. Выбор элементов из различных элементов, причем элементы могут повторяться: число возможных вариантов будет . Например, сколько различных пин-кодов из цифр можно придумать для банковской карты (см. рис. 21):

Рис. 21. Варианты различных пин-кодов из цифр для банковской карты

3. Размещение в определенном порядке без повторений некоторого количества элементов из множества (см. рис. 22). Если мы выбираем 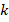элементов из общего количества различных элементов, то всего вариантов размещения будет:

Величина («а из эн по ка»), соответственно, называется числом размещений.

Рис. 22. Размещение элементов

4. Выбор в любом порядке некоторого количества элементов из множества (см. рис. 23). При выборе 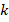элементов из элементов, вариантов выбора будет:

Величина («це из эн по ка») называется числом сочетаний.

Рис. 23. Сочетание элементов

Разница между размещениями и сочетаниями в следующем. При размещении важен порядок элементов, т. е. наборы 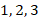и считаются различными. При сочетании порядок элементов не важен. Т. е. такие наборы считаются одинаковыми.

Например, при подсчете количества комбинаций при розыгрыше лотереи в начале урока ( номеров из ) нужно использовать формулу:

Использовали именно эту формулу, потому что порядок, в котором вы отметите номеров в билете, не важен.

Если бы выигрыш зависел еще и от порядка, то шанс победы в лотерее уменьшился бы еще в 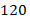раз:

Подробнее о выводе этих формул ниже.

 

Вывод формул

1. При выборе 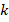элементов из общего количества с повторениями расчет простой: первый элемент выбираем способами, второй – тоже , аналогичной третий и т. д. до k -го. Получим:

2. Рассмотрим задачу на размещение элементов. Всего у нас есть элементов, нужно разместить 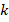из них (см. рис. 24).

Рис. 24. Всего есть элементов, нужно разместить 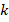из них

Первый элемент можно выбрать способами. Теперь у нас осталось элементов (см. рис. 25).

Рис. 25. Первый элемент можно выбрать способами, осталось элементов

Следующий элемент мы можем выбрать способом (см. рис. 26) и т. д.

Рис. 26. Второй элемент можно выбрать способами, осталось элементов

Очень похоже на расчет количества перестановок. Но там мы выбирали все элементы, и последний элемент выбирался однозначно. Т. е. произведение было до :

Здесь же у нас выбираются не все, а только 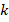элементов. После выбора элемента у нас останется элемент. Таким образом, последний, k -й, элемент мы можем выбрать 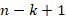способом. Произведение будет иметь вид:

Умножим и разделим это выражение на :

В числителе получили не что иное, как произведение всех натуральных чисел от до , т. е. :

3. Задача подсчета числа сочетаний похожа на расчет числа размещений. Мы выбираем 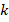элементов из элементов, но только здесь нам не важен порядок. Мы можем посчитать число размещений . Но поскольку нам не важен порядок, то некоторые варианты мы посчитали по несколько раз.

Например, мы выбираем буквы из латинского алфавита ( букв). При подсчете числа размещений варианты 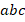, , , , , 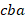различны. Но когда мы считаем количество сочетаний, нам важен лишь набор, но не порядок. Поэтому все эти вариантов должны быть посчитаны как . И это касается любой тройки букв. Таким образом, количество сочетаний будет в раз меньше количества размещений:

Почему именно число ? Мы получили это число, рассмотрев перестановки трех букв (, , , , , ):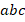

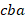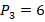
Таким образом:

Или в общем виде:

Подставив посчитанные ранее выражения для и , получим:

Решим задачу с использованием этих формул.

 

Задача 4. В классе 20 учеников. Найти количество способов:

а) выбрать команду из 6 человек на интеллектуальный турнир;

б) выбрать старосту и заместителя старосты класса;

в) выбрать трех учеников, которые за время урока пойдут к доске, если каждый ученик может выходить к доске неограниченное количество раз.

Решение.

а) необходимо выбрать 6 человек из 20 учеников. При этом порядок выбора не важен, важен сам набор участников. Это число сочетаний из 20 по 6:

Ответ можно упростить:

б) Выбирая старосту и его заместителя нам важен порядок, т. к. роли отличаются. Т. е. Петров – староста, Иванов – заместитель и Иванов – староста, Петров – заместитель – это разные варианты. Можно описать еще так: роль старосты – это «место 1», роль заместителя – «место 2». Нам нужно на этих местах разместить 2 учеников из 20. Это :

в) Нужно выбрать учеников из . Причем один и тот же ученик может выходить к доске несколько раз. Это выбор из по с повторениями. Всего будет вариантов:

Ответ: .

Случайные события

Мы живем в вероятностном мире. Вокруг происходят различные случайные события, и случайными их называют потому, что их очень сложно или практически невозможно предсказать.

Погода на улице, результаты спортивных соревнований, результаты лотереи – все это случайные события. Да, можно сделать прогноз погоды, основываясь на данных о давлении и температуре, или сказать, что фаворит выиграет у аутсайдера. Но нельзя гарантировать, что в точности так это и произойдет.

И в этом мы неоднократно убеждаемся: синоптики могут предсказать на завтра дождь, но целый день будет солнечно, букмекеры будут отдавать победу Испании, но дальше пройдет сборная России.

Классическим примером случайного события является подбрасывание монетки и выпадение «орла» или «решки». И здесь можно попробовать рассчитать, что выпадет: смоделировать физическую ситуацию, сделать расчет. Но результат будет напрямую зависеть от начальных условий: высоты над поверхностью и скорости броска. А эти условия случайны: чуть сильнее бросил, чуть выше отпустил – и уже вместо «орла» выпадает «решка».

Базовые понятия о вероятности необходимы каждому человеку. Они помогут понять, что даже зимой крайне мала вероятность, что все учителя заболеют и вам не придется идти в школу. А знания элементарных формул теории вероятности объяснят, что не стоит ставить в лотерее рублей, если можно выиграть миллион с вероятностью одна миллионная.