Распределение Пуассона является предельным законом для распределения Бернулли.
Случайная величина может принимать значения от 0 до3.
Плотность распределения и функция распределения равномерной случайной величины, ее числовые характеристики.
Часто встречаются случайные величины, которые могут принимать значения только в строго определенных границах некоторого отрезка [a;b], причем с содержательной точки зрения все значения внутри этого отрезка равновозможны. Например, минутная стрелка остановившихся механических чатов будет показывать какое-то значение; заранее, до поломки, неизвестно, какое именно, но точно известно, что оно будет в пределах от 0 до 60. Погрешность округления также относится к подобным величинам. О таких величинах говорят, что они распределены по равномерному закону на некотором отрезке [a;b].
Более строго, случайная величина Х с функцией распределения
F(x) = 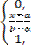
(К данным значениям относятся условия:
- к первому: x<a
- ко второму:a 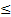 x<b
x<b
- к третьему: x 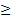 b)
b)
Называется распределенной по равномерному закону на отрезке [a;b]. Плотность распределения этой случайной величины получается путем дифференцирования:
f(x) = 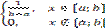
Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения (^ - местами, где не получилось сделать верхний индекс, этим знаком обозначена степень)
b
MX = 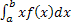 =
= 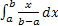 =
= 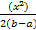 | =
| = 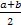
a b
MX2 = 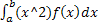 =
= 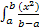 =
= 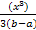 | =
| = 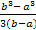 =
= 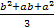
a
DX = MX2 – (MX)2 = 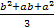 -
- 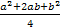 =
= 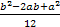 =
= 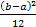
Среднее квадратическое отклонение
σX = 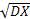 =
= 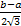
Вероятность попадания случайной величины в заданный интервал:
P (α<X<β) = 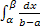 =
= 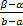
Плотность распределения и функция распределения показательной случайной величины, ее числовые характеристики.
Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
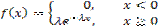
где - положительное число
Найдем закон распределения
F(x) = 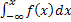 =
= 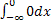 + λ
+ λ 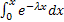 = 1- e-λx
= 1- e-λx
F(x) = 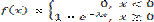
Интервал времени между двумя последовательными появлениями некоторого редкого события описывается случайной величиной, распределенной по показательному закону. Например, по показательному закону распределено время безотказной работы какого-либо устройства.
Найдем математическое ожидание и дисперсию.
∞
MX = 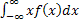 =
= 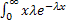 dx =
dx = 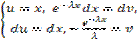 = λ(-
= λ(- 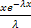 | +
| + 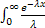 dx =
dx =
0
∞
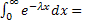 -
- 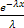 | =
| = 
0
Результат получен с использованием того факта, что
∞
xe-λx | = 0
0
Для нахождения дисперсии найдем величину MX2
MX2 = 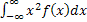 =
= 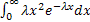
Дважды интегрируя по частям получаем
MX2 = 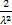
Тогда DX = MX2 – (MX)2 = 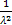
σX = 
Видно, что в случае показательного распределения математическое ожидание и среднее квадратическое отклонение равны.
Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.
P(a<X<b) = F(a) – F(b) = e-λa – e-λb
Показательное распределение широко используется в теории надежности.
 2020-05-21
2020-05-21 197
197








