В ряде задач о размещении пунктов обслуживания требуется так расположить пункт обслуживания в графе, чтобы сумма кратчайших расстояний от этого пункта до вершин графа была минимально возможной. Оптимальное в указанном смысле место расположения пункта называется медианой графа. Исходя из природы целевой функции, такие задачи называются минисуммными задачами размещения. Эти задачи в различных формах часто встречаются на практике. В дипломной работе решается задача построения оптимальной структуры типа «радиально-узловая» с использованием минисуммной задачи размещения.
Следует отметить, что при расчетах структур комбинированных сетей может использоваться минимаксная задача размещения. В этом случае используется задача о нахождении р-медианы данного графа G; это задача об оптимальном размещении заданного числа выделенных узлов графа (центров коммутации), при котором сумма кратчайших расстояний от вершин графа до ближайших к ним пунктов принимает минимально возможное значение. Задача нахождения р-медианы может быть несколько обобщена, если каждой вершине xj сопоставить некоторый вес vj (представляющий, например, ее размеры или важность); тогда целевой функцией, подлежащей минимизации, станет сумма «взвешенных» расстояний.
|
|
|
Пусть дан граф G=(X, Г). Для каждой вершины xi€X определим два числа, которые назовем передаточными числами:

где, d(xi, xj) – кратчайшее расстояние от вершины xi до вершины хj. Числа σо(xi) и σt(xi) называются соответственно внешними и внутренними передаточными числами вершины хi. Число σо(xi) есть сумма элементов строки хi матрицы, полученной после умножения каждого столбца матрицы расстояний D(G) = [d(xi, xj)] на вес соответствующий этому стобцу вершины, т.е. j-й столбец умножается на vj; число σt(xi) есть сумма элементов столбца хi матрицы, полученной в результате умножения каждой строки матрицы расстояний D(G) на соответствующий этой строке вес (j-я строка умножается на vj).
Вершина  , для которой
, для которой

называется внешней медианой графа G, а вершина  , для которой
, для которой
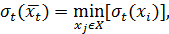
называется внутренней медианой графа G.
В качестве примера в дипломной работе рассмотрен граф, изображенный на рисунке (для которого все vj и cij приняты равными единице), и вычислим внешние и внутренние передаточные числа вершин.
Эти числа приведены в присоединенных к матрице расстояний строке и столбце:
| x1 | x2 | x3 | x4 | x5 | x6 | σо(xi) | |
| x1 | 0 | 1 | 2 | 3 | 2 | 3 | 11 |
| x2 | 3 | 0 | 1 | 2 | 1 | 2 | 9 |
| x3 | 4 | 3 | 0 | 1 | 2 | 3 | 13 |
| x4 | 3 | 2 | 2 | 0 | 1 | 2 | 10 |
| x5 | 2 | 1 | 1 | 2 | 0 | 1 | 7* |
| x6 | 1 | 2 | 3 | 4 | 3 | 0 | 13 |
| σt(xi) | 13 | 9* | 9* | 12 | 9* | 11 |
Рис.31 расчет передаточных чисел графа G.
|
|
|
По полученным передаточным числам видно, что внешней медианой графа является х5 с σо(x5)=7 и что существует три внутренние медианы (х2, х3 и х5), каждая с внутренним передаточным числом, равным 9 [3].
Вывод по главе
Во второй главе рассмотрены основные алгоритмы, используемые при решении оптимизационной задачи. При расчете одно-, двух- и трех кольцевых структур применяется алгоритм «Коммивояжер», который заключается в нахождении минимального гамильтонова цикла. По данному алгоритму рассчитывается и «линейная» структура сети, отличие в том, что минимальный гамильтонов цикл необходимо преобразовать в минимальный гамильтонов путь путем удаления ребра наибольшей длины. Решение является приближенным.При оптимизации структур решается минисуммная задача, которая заключается в нахождении передаточных чисел графа и выбора среди них минимального, что является решением. Алгоритм решения является полиномиальным, составлена программа «Расчет и поиск медианы графа».
 2020-05-21
2020-05-21 190
190








