Алгоритм «Коммивояжер»

Успешное функционирование сетей связи специального назначения (СС СН), обеспечивающих выполнение задач управления войсками и оружием, во многом определяется выбранным программным обеспечением (ПО). К нему предъявляется целый ряд требований, основными из которых являются: высокая точность осуществляемых расчетов; время вычисления, не превышающее заданное; защищенность от кибер атак противника и др.

К сожалению, многие из задач, входящих в ПО СС СН, такие как: формирование баз данных; распределение каналов и сетевых потоков; распределение длин волн в оптических сетях; оценка живучести сетей, относятся к классу «трудно решаемых». Точное решение данных задач может быть найдено переборными методами, которые выполняются за время, существенно большее, чем время, отводимое на их расчёт. Это требует разработки и использования приближенных алгоритмов, которые позволяют с некоторой (достаточной) точностью решать задачи данного класса в рамках временного ресурса. Причем данные алгоритмы обладают рядом специфических («коварных») особенностей. Прежде всего, для них характерно условие: чем выше заказанная точность решения, тем больше времени может требоваться на работу алгоритма. С другой стороны, алгоритмы данных задач весьма критичны к заданию исходных данных (выбору структур сетей и их параметров). Так, например, алгоритм, который успешно решает задачи некоторого класса сетей, может грубо ошибаться при незначительных изменениях исходных данных в структуре сети или ее параметрах. По этой причине их использование возможно только при проведении тестирования разрабатываемых алгоритмов в рамках множества вариантов исходных данных, что характерно для СС СН. В теории трудно решаемых задач авторами всесторонне изучены эти проблемы и выработаны рекомендации по составлению и оценке алгоритмов их решения. По мнению данных авторов, наиболее эффективным является метод «ветвей и границ», используемый при решении задачи «Коммивояжера». Как показал опыт расчета параметров СС СН, именно алгоритм решения задачи «Коммивояжера» является наиболее эффективным и может быть рекомендован при составлении ПО СС СН.

Рассмотрим задачу «Коммивояжера» на простом примере. «Коммивояжеру» требуется посетить каждый город в пределах конкретной зоны обслуживания и возвратиться домой. Не приходится и говорить, что «Коммивояжеру» хотелось бы выбрать такой порядок обхода клиентов, при котором его путь был возможно короче. Таким образом, «Коммивояжер» сталкивается с задачей поиска маршрута минимальной протяженности, длительности или стоимости.

Математически задача «Коммивояжера» может быть сформулирована, как задача на графе в следующей постановке: построить граф G(X, A), вершины которого соответствуют городам в зоне «Коммивояжера», а дуги отображают коммуникации, соединяющие пары городов. Пусть длина a(x, y)≥0 каждой дуги (x, y)€A равна расстоянию, стоимости или времени. Контур, включающий каждую вершину графа G хотя бы один раз, называется маршрутом «Коммивояжера». Контур, включающий каждую вершину графа G ровно один раз, называется гамильтоновым контуром.

Общей задачей «Коммивояжера» называется задача поиска маршрута наименьшей общей длины (задачей коммивояжера называется задача поиска гамильтонова контура наименьшей общей длины).

ПРИМЕР. В цехе, имеющем n различных станков, изделие должно быть обработано на каждом из n станков в некоторой произвольной последовательности. При этом время переналадки, необходимое для передачи изделия от станка х к станку у, равно а(х, у). Какую выбрать последовательность обработки на каждом из станков, для того чтобы минимизировать общее время обработки изделия?

Эта задача решается как задача «Коммивояжера» на графе G, каждая вершина которого соответствует станку, а каждая пара (х, у) вершин соединяется дугой, имеющей длину а(х, у). Контур «Коммивояжера», имеющий наименьшую длину, называется оптимальным маршрутом «Коммивояжера» и является оптимальным решением общей задачи «Коммивояжера». Гамильтонов контур наименьшей длины называется оптимальным гамильтоновым контуром и является оптимальным решением задачи «Коммивояжера».                               

 

 

 

 

Рис.11. Ориентированный граф.

 

 

Оптимальный маршрут «Коммивояжера» не обязательно является гамильтоновым контуром. Например, рассмотрим граф, показанный на рис. 11. В этом графе имеется только один гамильтонов контур (а, b), (b, c), (c, a) с общей длиной, равной 20+1+1=22. Оптимальный же маршрут «Коммивояжера» (a, b), (b, a), (a, c), (c, a) проходит через каждую вершину дважды и имеет общую длину 1+1+1+1=4.

Возникает вопрос, в каких случаях гамильтонов контур является решением общей задачи «Коммивояжера»?

ТЕОРЕМА. Если для каждой пары вершин (х, у) графа G выполняется условие а(х, у)≤a(x, z) + a(z, y) для всех z≠x, z≠y, то гамильтонов контур является решением общей задачи «Коммивояжера» на графе G (если решение вообще существует). Это условие говорит только о том, что расстояние непосредственно от х до у никогда не превышает расстояния от х до у через любую другую вершину z и называется условием неравенства треугольника.

Предположим, что мы желаем вместо гамильтонова контура наименьшей длины найти гамильтонов контур, имеющий максимальную длину. Например, банковский курьер пожелает максимизировать, а не минимизировать общее количество доставляемых им дополнительных писем. Может ли эта задача быть сведена к задаче «Коммивояжера»?

Пусть через М обозначена наибольшая длина дуги в графе G. Пусть далее a^’ (x, y) = M – a(x, y)≥0 для всех дуг (х, у). Каждый гамильтонов контур на графе G=(X, A) содержит ровно |X| дуг. Оптимальный (в смысле наименьший длины) гамильтонов контур С включает дуги, преобразованные в соответствии с соотношением указанным выше, и его общая длина равна 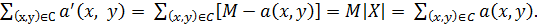 Таким образом, гамильтонов контур минимальной длины, состоящий из преобразованных дуг, эквивалентен гамильтонову контуру максимальной длины, составленному из тех же дуг с исходной длиной [4].

Известны многие различные методы решения задачи «Коммивояжера». Среди них можно выделить методы, разработанные Беллмором и Немхаузером, Гарфинкелем и Немхаузером, Хелдом и Карпом, Стекханом. Все эти методы относятся к одному из двух классов:

· Методы, которые всегда приводят к нахождению оптимального решения, но требуют для этого в наихудшем случае недопустимо большого числа операций.

· Методы, которые не всегда приводят к нахождению оптимального решения, но требуют для получения такого решения приемлемого числа операций.

Метод «ветвей и границ» относится к первому классу методов решения задачи «Коммивояжера», второй – метод последовательного улучшения решения – ко второму классу [5].

Евклидизация

В дипломной работе в соответствии с требованиями теоремы 1 разработан способ перевода исходных данных решения задачи коммивояжера к метрике Евклида. Данное обстоятельство используется при решении ряда сетевых задач военной связи. В теории гамильтоновых сетей класс Евклидовых сетей известен. Он имеет достаточно жесткие ограничения на отношения между весами ребер сети. Так, если для любых трех связанных ребер сети (рис. 12) выполняются соотношения: то такие сети называются Евклидовыми.

Рис.12. Евклидовая сеть.

C_ij + C_jk ³ C_ik; C_jk + C_ik ³ C_ij; C_ik + C_ij ³ C_jk;

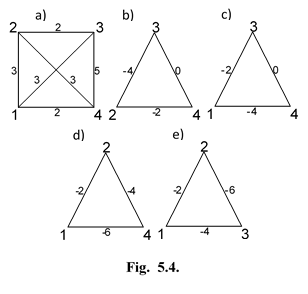i, j, k Î N;    i ¹ j ¹ k;    C_ij, C_jk, C_ik ³0,            (1)

 

Кроме того, Евклидовыми могут быть сети, у которых ребра имеют отрицательный вес. При этом соотношения между весами этих ребер должны принимать следующий вид:

 

C_ij ³ C_jk + C_ik; C_jk ³ C_ik + C_ij; C_ik ³ C_ij + C_jk;

                  i, j, k Î N;   i ¹ j ¹ k;  C_ij, C_jk, C_ik £ 0.       (2)

 

Не могут быть Евклидовыми и не требуют проверки сети, у которых веса ребер являются как положительными, так и отрицательными числами.

В дальнейшем Евклидовые сети будем обозначать как G~ _N.

Рассмотрим вначале некоторые достаточно очевидные свойства Евклидовых сетей.

Cвойство 1. Если в G~   _N выполнено преобразование R (i), i =1÷ N, то образованные сети могут не быть Евклидовыми.

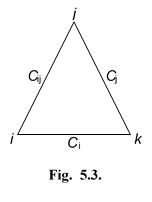Справедливость данного утверждения проиллюстрируем следующим примером.

 

Рис.13. Преобразование графа G.

 

Рис.13

Пусть в G~   ₄ (рис. 13, а) выполнено преобразование R (i), i =1÷4 и образованы сети G~ _{4 - (i)} (рис. 13, б - д). Можно проверить, что сети, изображенные на рис. 13, б, в не являются Евклидовыми, поскольку для них не выполняются соотношения (1). Так, например, для сети на рис. 13, б C ₂₃< C ₂₄+ C ₃₄, что противоречит условию, определяющему класс Евклидовых сетей. В то же время сети, изображенные на рис. 13, г, д, остались таковыми и после преобразования G~ ₄.

Таким образом, мы убедились, что преобразование R (i) сети G~   _N приводит к появлению сетей G~ _{N - (i)}, которые могут не быть Евклидовыми.

Свойство 2. Если в G~   _N удаляются один, два и большее число произвольным образом выбранных узлов (или G~   _N делится на части), то все образованные сети (части сети), в которых число узлов больше или равно трем, остаются Евклидовыми.

Доказательство. По определению Евклидовых сетей для ребер, связывающих любые три узла, выполняется «правило треугольника». Тогда, если в G~   _N выделяется часть сети с числом узлов больше трех, то в силу условий определения данного класса выделенная сеть может быть только Евклидовой.

Рассмотрим следующий пример.

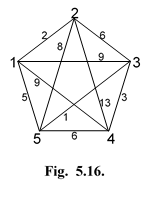
Пример 1. На рис. 14 изображена Евклидова сеть с N =5. Требуется проверить, являются ли Евклидовыми сети, образованные путем удаления в G~ ₅ одного и двух узлов.

        

 

 

                                                                                              

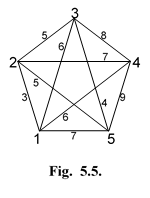
Рис.14. Евклидова сеть с N=5.

 

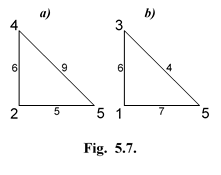
На рис. 15 показаны сети, образованные из G~ ₅ путем удаления в ней одного из узлов (от первого до пятого).

 

 

 

Рис.15

 

Рис.15. Образованные сети путем удаления одного из узлов.

 

Можно проверить, что все указанные сети являются Евклидовыми, поскольку соотношения между весами ребер в них сохранились такими же, как в исходной сети. Не менялись соотношения между весами соответствующих ребер в сетях, образованных при удалении в G~   ₅ пар узлов 1, 3 и 2, 4 (рис. 16, а, б). Следовательно, преобразование исходной сети путем удаления в ней узлов не меняет соотношений между весами ребер в любых частях сети (по сравнению с теми, которые были в G~ ₅) и образованные таким образом сети остаются Евклидовыми.

Рис.16

Перейдем к более важной части наших рассуждений об Евклидовых сетях. Выясним механизм преобразования сетей общего вида в Евклидовы.

 

 

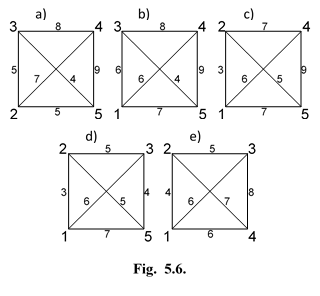
Рис.16. Евклидовы сети.

Свойство 3. Сеть общего вида может быть переведена в класс Евклидовых путем увеличения (или уменьшения) весов ребер этой сети на некоторую величину D.

Доказательство. Предположим, в G~   _N определена некоторая величина        D = [ C_ik - (C_ij + C_jk)] = max, i, j, k Î N; i ¹ j, i ¹ k, являющаяся показателем неевклидовости данной сети. Причем максимальное значение находится из показателей неевклидовости всех возможных треугольных соединений ребер сети. Увеличим веса ребер сети на величину D. Для «треугольника», в котором D=max, будем иметь C_ik +D= C_ij + C_jk +2D, т. е. C¢_ik = C¢_ij + C¢_jk, что соответствует условию (1), и сеть с новыми весами ребер становится Евклидовой. При этом условие (1) автоматически выполняется для всех других ребер сети, соединенных в виде треугольников.

Величина, на которую следует изменить веса ребер сети для перевода ее в класс G~   _N, необязательно должна быть равна D. Действительно, выбирая эту величину достаточно большой [больше max C (G~   _N) - 2min C (G~   _N)], всегда можно добиться выполнения условия (1). Аналогичным образом можно доказать, что и уменьшение весов ребер сети на некоторую величину также приводит к переводу G~   _N в класс Евклидовых.

К сожалению, данный способ Евклидизации сетей мало что может дать, поскольку с его помощью не устраняется «зашумляющее» действие ребер. Сказанное подтверждается свойством 2, согласно которому утверждается, что изменение весов ребер, инцидентных любым узлам исходной сети, в том числе и их увеличение на одну и ту же величину, не влияет на веса ребер сети, образованной с помощью преобразования R (i). Поскольку в работе оптимизационных алгоритмов используются сети G~   _{N -(i)} или G~   _{N - (n = j)}, синтезируемые с помощью преобразования R (i), то любые предварительные изменения исходной сети (в рамках рассматриваемого способа Евклидизации) являются не информативными.

Пример 2. На рис. 17 изображена сеть, которую требуется перевести в класс Евклидовых.

        

 

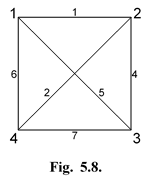
Рис.17. Сеть, которую необходимо перевести в класс Евклидовых.

 

Поскольку для сети с большим числом узлов N поиск максимального значения D является достаточно сложной процедурой, то D можно заменить величиной max C (G~   _N) - 2min C (G~ _N), определение которой существенно проще. Для сети, представленной на рис 17, max C (G~  ₄)=7, min C (G~  ₅)=1. Тогда max C (G~  ₅) - 2min C (G~  ₅)=5 [для сравнения в рассматриваемой сети D=(6 - (2+1)=3].

 

Увеличим веса ребер исходной сети на 5 единиц и образуем Евклидову сеть (рис. 18).

 

 

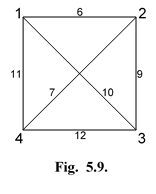
Рис.18. Сеть с увеличенными весами ребер.

 

 

Выше отмечалось, что с позиции преобразования R (i) сети, изображенные на рис. 17 и 18, являются эквивалентными. Покажем это.

 

 

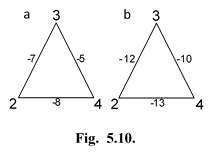
Рис.19. Синтезированные сети.

 

С этой целью преобразование R (i) выполним для двух указанных сетей и синтезируем сети, показанные на рис. 19, а, б. Веса ребер этих сетей отличаются лишь плоским уровнем в пять единиц на который они понижены в сети, изображенной на рис. 19, б.

По этой причине перевод сети G~  ₅ в G~   ₅, как мы убеждаемся, не может решить задачу устранения «зашумляющего» действия ребер.

Перейдем к рассмотрению более сложной процедуры Евклидизации сетей G~   _N. Желаемый результат в рассмотренном выше способе Евклидизации достигается увеличением весов всех ребер сети на некоторую величину. Однако такого же результата можно достичь путем уменьшения весов ребер, которые выходят за рамки соотношений (1).

Предположим, для некоторой тройки ребер, связывающих в G~   _N узлы i, j, k, C_ij > C_jk + C_ik. Если C_ij уменьшить на величину d= C_ij - (C_jk + C_ik), то соотношения (5.3) будет выполняться и, по крайней мере в рамках выделенной тройки ребер, сеть является Евклидовой. Однако такое решение не может быть окончательным, поскольку требуется проверить все тройки ребер, куда входит ребро r (i - j). Только определив для данного ребра d=max, можно окончательно принять решение о его весе в преобразованной сети, а именно: C¢_ij = C_{ij - (d=max)}. Процедура C¢_ij = C_{ij - (d=max)} дает возможность пересчета весов всех ребер сети и перехода к следующему этапу проверки и преобразования. При этом i, j, k Î N; i ¹ j ¹ k.

К сожалению, однократное выполнение операции определения d=max и пересчета весов ребер сети не всегда приводит к образованию G~   _N.

 

На рис. 20, а изображен фрагмент сети, для которого условия (1) выполняются только после завершения третьей операции преобразования.

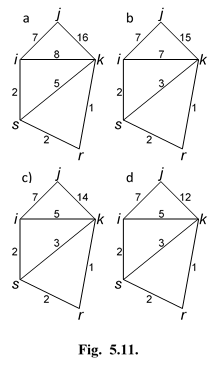
Рис.20. Фрагмент исследуемой сети.

 

Первая операция (рис. 20, б):

C¢_jk = C_jk - (C_ij + C_ik)=15,

C¢_ik = C_ik - (C_is + C_sk)=7,

C¢_sk = C_sk - (C_sR + C_kR)=3.

Вторая операция (рис. 20, в):

C¢¢_jk = C¢_jk - (C_ij + C¢_ik)=14,

C¢¢_ik = C¢_ik - (C_is + C¢_sk)=5,

C¢¢_sk = C¢_sk - (C_sr + C_kr)= 3.

Третья операция (рис. 20, г):

C¢¢¢_jk = C¢¢_jk - (C_ij + C¢¢_ik)=12,

C¢¢¢_ik = C¢¢_ik - (C_is + C¢¢_sk)=5,

C¢¢¢_sk = C¢¢_sk - (C_sr + C¢¢_kr)=3.

 

Легко подсчитать, что в сети с N узлами максимальное число операций, после выполнения которых сеть преобразуется в G~ _N, составит N - 2.

Изложим алгоритм Евклидизации сетей, в основу которого положено преобразование R (i).

 

Рис.20

Алгоритм «Евклидизация»:

1. Для заданной сети G~   _N выполнить операцию R (i), i =1÷ N и образовать сети G~   _{N - (i)}.

2. В каждой из сетей G~   _{N - (i)} определить ребра, вес которых больше нуля

3. Определить: max _i .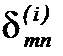

4. В G~   _N веса соответствующих ребер уменьшить на величину max 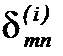. Перейти к п. 1, считая найденную сеть исходной.

Алгоритм заканчивает работу после выполнения операции п. 4, если max 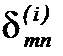 £ 0; m, n Î N; m ¹ n.

Определим верхнюю границу сложности алгоритма «Евклидизация».

Как следует из описания алгоритма, в нем можно выделить три самостоятельные процедуры. Известно, что преобразование R (i) выполняется с помощью алгоритма «Равенство», сложность которого 1,5 N ². При i =1÷ N число преобразований сети увеличивается до N, а сложность первой процедуры становится равной 1,5 N ³.

Вторая процедура связана с нахождением max 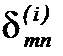, m, n Î N; m ¹ n; i =1÷ N. Число групп элементов (весов ребер), среди которых ищется max 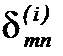, определяется числом ребер сети и составляет 0,5 N (N - 1). Число элементов в каждой группе равно N - 2. Если при сравнении двух чисел и выборе большего требуется выполнить четыре простейшие операции, то сложность второй процедуры будет определяться как 0,5 N (N - 1)´(N - 2)´4.

Наконец, третья процедура связана с уменьшением весов ребер G~   _N (тех из них, для которых max 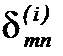> 0).

Предположим, в G~   _N требуется уменьшить веса всех ребер на величину max 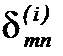. Это выполнимо с помощью 2´0,5 N (N - 1) простейших операций.

Тогда сложность одного цикла алгоритма будет определяться суммой найденных величин для каждой процедуры в отдельности, а именно:

 

1,5 N ³+2 N (N - 1)(N - 2)+ N (N - 1).        (3)

 

Известно, что при определенных весах ребер исходной сети за один цикл синтезировать сеть G~   _N невозможно. В общем случае требуется выполнить не более N - 2 циклов. Следовательно, верхняя граница сложности алгоритма «Евклидизация» будет равна произведению числа циклов на число простейших операций, выполняемых в одном цикле, и составит величину

 

(N - 2)´[1,5 N ³+ N (N - 1)(N - 2)+ N (N - 1)].       (4)

                   

Отметим возможные пути уменьшения сложности алгоритма «Евклидизация».

Это осуществимо за счет изменения порядка выполнения процедур в цикле. Так, например, сложность алгоритма может быть снижена при следующем порядке его работы:

1. Выполнить операцию R (i), i =1.

2. В G~ _{N - (i)} определить ребра, вес которых больше 0.

3. В заданной сети G~   _N уменьшить соответствующие ребра на величину превышения, установленную в п. 2.

4. Перейти к п. 1, приняв i =2, и т. д.

Кроме того, при работе алгоритма «Евклидизация» можно исключить из рассмотрения любую тройку ребер сети, если на предыдущем цикле их веса не изменялись.

Пример 3. На рис.21 изображена сеть G~ ₇.

        

 

 

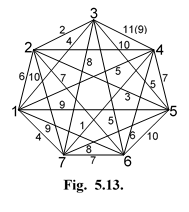
Рис.21. Граф G7.

 

С помощью алгоритма «Строительство 1» найден цикл H_g (5 - 2 - 1 - 3 - 6 - 4 - 7 - 5). Требуется, используя алгоритм «Евклидизация», перевести заданную сеть в класс G~   ₇ и улучшить цикл H_g.

1. Для заданной сети выполним преобразование R (i), i =1÷7 и найденные значения весов ребер сетей G~ _{7 - (i)} поместим в табл. 1.

2. Определим max _i 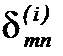> 0 (см. последний правый столбец табл. 1).

3. В исходной сети уменьшим веса соответствующих ребер на величину max _i 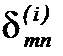 и образуем сеть, показанную на рис. 22. Считая найденную сеть исходной, перейдем в соответствии с алгоритмом к п. 1.

 

 

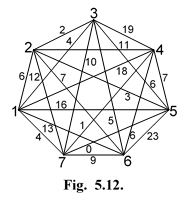
Рис.22. Образованный граф.

 

Таблица 1.

Значение весов ребер графа G₇.

Веса ребер	Сети G~ 7-(i)							max i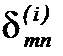
сети	i =1	i =2	i =3	i =4	i =5	i =6	i =7
C 12			0	-23	-13	-14	-10
C 13		-4		-33	-18	-14	-10
C 14		1	-5		-5	-1	13	13
C 15		7	6	-9		-20	4	7
C 16		0	4	-11	-26		0	4
C 17		-14	-10	-15	-20	-18
C 23	-8			-28	-7	-10	-20
C 24	-13		-10		1	-2	-2	1
C 25	-19		-5	-18		-27	-17
C 26	-12		0	-10	-19		-14
C 27	2		-4	0	1	-4		2
C 34	-3	6			6	8	8	8
C 35	-14	1		-20		-22	-12	1
C 36	-12	-4		-20	-24		-14
C 37	2	-4		-10	-4	-4		2
C 45	-27	-7	-18			-22	-2
C 46	-25	-12	-18		-24		-4
C 47	-21	-22	-28		-14	-14
C 56	-6	13	12	10			6	13
C 57	-12	-5	-8	0		-24
C 67	-8	-10	-6	2	-22			2

Однако мы ограничимся рассмотрением лишь одного цикла алгоритма и укажем, что в процессе выполнения второго цикла корректируется лишь вес ребра r (3 - 4) (уменьшается с 11 до 9). Других изменений в сети, изображенной на рис. 5.13, не происходит. Данная сеть с C ₃₄=9 и является Евклидовой, т. е. искомой.

Следует заметить, что данный вариант Евклидизации может выполняться при различных плоских уровнях, устанавливаемых в G~   _N. В рассматриваемом примере перед выполнением алгоритма «Евклидизация» веса ребер сети не изменялись, что соответствует нулевому уровню. Если перед выполнением данного алгоритма веса ребер увеличивались (уменьшались) на некоторую величину, то эта величина и определяет его значение. Очевидно, что плоский уровень не должен превышать величины D, при которой сеть переводится в класс евклидовых, и последующая работа алгоритма «Евклидизация» теряет смысл.

Таким образом, первая часть задачи решена — образована Евклидова сеть, изображенная на рис. 22. С помощью алгоритма «Строительство 1» выполним улучшение заданного цикла.

 

На рис. 23 показана работа данного алгоритма. В результате работы алгоритма выполняется размещение узла 1 между узлами 5 и 7. При этом

 

 

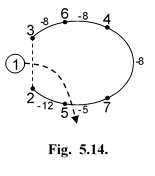
Рис.23. Работа алгоритма.

 

образуется цикл H (2 - 5 - 1 - 7 - 4 - 6 - 3 - 2), длина которого на три единицы меньше, чем цикла заданного.

Пример 4. На рис. 24 изображена сеть G~  ₅. Требуется, используя алгоритм «Евклидизация», перевести ее в класс евклидовых при двух значениях плоского уровня: 0, - 4.

        

 

 

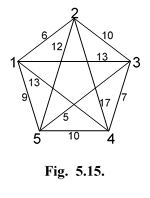
Рис.24. Граф G5.

 

В табл. 2 указаны веса ребер сетей G~  _{5 - (i)}, i =1-5, найденных с помощью преобразования R (i). Как видно из таблицы, веса ребер всех сетей не больше нуля. Это дает основание считать заданную сеть Евклидовой.

 

Таблица 2.

Веса ребер сетей G_5-(i).

Сети	Веса ребер сети
G~ 5-(i)	C 12	C 13	C 14	C 15	C 23	C 24	C 25	C 34	C 35	C 45
G~ 5-(1)					-9	-2	-3	-19	-17	-12
G~ 5-(2)		-3	-10	-9				-20	-17	-19
G~ 5-(3)	-17		-7	-9		0	-3			-2
G~ 5-(4)	-24	-7		-14	-14		-15		-12
G~ 5-(5)	-15	-1	-6		-7	-5		-8

Таким образом, данная сеть при нулевом плоском уровне является Евклидовой и изменять веса каких - либо ее ребер не требуется.

Перейдем к решению той же задачи при втором значении плоского уровня.

С этой целью предварительно уменьшим веса ребер сети (рис. 24) на четыре единицы и получим сеть, показанную на рис. 25.

 

 

Рис.25. Преобразованный граф G5.

 

Выполним преобразование R (i), i =1÷5 указанной сети и образуем семейство сетей G~  _{5 - (i)} (рис. 26, а — д).

 

 

Рис.26. Семейство сетей G_5-(i).

 

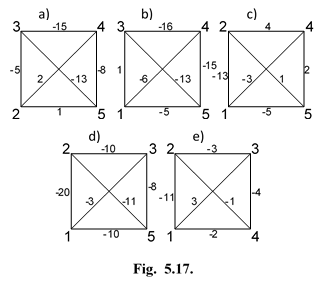Поскольку данные сети содержат ребра, веса которых больше нуля, то рассматриваемая сеть не является Евклидовой. Для ее перевода в класс Евклидовых необходимо дополнительно к преобразованию R (i) выполнить ПП. 2, 3 и 4 алгоритма «Евклидизация».

Рис.26

        

Определим max _i 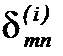 (max 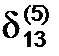=3, max 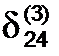=4, max 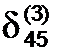=2, max 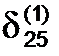=1).

 

 

 

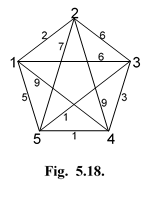
Рис.27. Сеть, после второго цикла алгоритма.

 

Уменьшив веса C ₁₃, C ₂₄, C ₄₅ и C ₂₅ ребер сети (рис. 25) на max _i 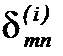, получим сеть, показанную на рис. 27. Выполнив второй цикл алгоритма «Евклидизация», можно показать, что данная сеть является Евклидовой.

В данном примере изменялся плоский уровень для всей сети. Следует отметить, что предварительно можно изменять уровень весов не только всех ребер сети, но и ребер, инцидентных какому - либо одному, двум и т. д. ее узлам.

Согласно свойству 2, данные преобразования являются эквивалентными, и они не меняют ранжирования и прохождения гамильтоновых циклов сети. Так, например, в сети, показанной на рис. 24, предварительно перед выполнением алгоритма «Евклидизация» можно уменьшить веса ребер, инцидентных какому - либо одному (или двум, трем и т. д.) ее узлу (узлам), на четыре единицы. Важно еще раз отметить, что исходная и измененная сети в смысле ранжирования гамильтоновых циклов остаются эквивалентными.

К сказанному добавим, что предварительные изменения весов всех ребер сети (или инцидентных некоторым ее узлам) не должны приводить к появлению в G~   _N ребер с отрицательными весами. Если же в исходной сети уже имеются такие, то величина плоского уровня сети (или плоского уровня для ребер, инцидентных некоторым узлам) должна выбираться исходя из требования положительности весов всех ее ребер. Существует некоторое предельное значение весов ребер сети, которое не может быть изменено перед выполнением алгоритма «Евклидизация». Суть этого состояния сети заключается в том, что каждому ее узлу должно быть инцидентно, как минимум, одно ребро минимального веса. Причем все эти ребра могут иметь одинаковый минимальный вес. Достигается указанное состояние сети последовательным уменьшением или увеличением весов ее ребер, инцидентных каждому узлу.

Так, например, сеть, изображенная на рис. 28, может быть преобразована путем уменьшения весов ребер, инцидентных узлам (четвертому — на 10, пятому — на 2, первому — на 3, шестому — на 4).

 

 

 

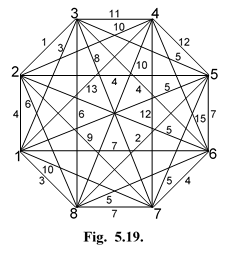
Рис.28. Сеть с N=8.

 

Данное состояние сети (рис. 29) можно принять как предельное, поскольку каждому узлу инцидентно, как минимум, одно ребро с единичным весом. Эту операцию можно характеризовать как выравнивание весов ребер МОД, которое устанавливается в данной преобразованной сети.

 

 

 

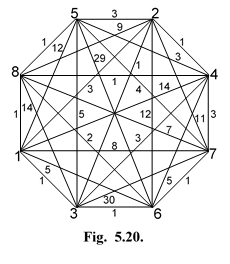
Рис.29. Предельное состояние сети.

 

Следует заметить, что порядок узлов с изменяющимися весами ребер можно выбирать произвольным образом. Для той же сети (рис. 28) желаемый результат может быть достигнут, если изменения производить в узлах в соответствии с их нумерацией (веса ребер, инцидентных первому узлу, уменьшить на 3, второму — на 1, четвертому — на 9, пятому — на 2, шестому — на 4). В нашем перечислении узлы 3, 7, 8 опущены, поскольку изменение весов их ребер при выбранном порядке преобразования становилось невозможным.

На рис. 30 показана G~   ₈, образованная с помощью алгоритма «Евклидизация» из сети, изображенной на рис. 29.

 

 

 

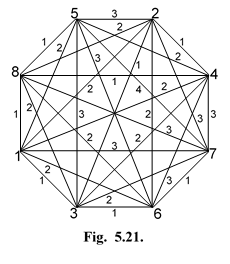
Рис.30. Сеть G8.

 

Введение понятия «предельное состояние сети» диктуется двумя обстоятельствами. Во - первых, исходная сеть и преобразованная являются эквивалентными в смысле ранжирования гамильтоновых циклов. Во - вторых, сеть, у которой ребра МОД имеют одинаковые веса, достаточно простым способом преобразуется в Евклидову (с помощью процедур, сложность которых меньше, чем сложность алгоритма «Евклидизация») [6].