Задача 1. Найти графически оптимальное решение системы неравенств:
2x1 + x2 > 2 (1)
x1 + 3x2 > 3 (2)
x1 – x2 > -1 (3)
3x1 – x2 < 6 (4)
x1 + x2 < 5 (5)
x1 > 0 (6)
x2 > 0 (7)
максимизирующее целевую функцию:
F = x1 + 2x2 (8)
Решением задачи являются такие x1 и x2, при которых целевая функция будет максимальной.
Этапы решения:
1. Строим систему координат X1OX2.
2. Определяем вид каждого из ограничивающих условий (1-7) в этих координатах. При этом каждое нестрогое неравенство разделяем на строгое равенство и строгое неравенство. Вместо неравенства (1) рассмотрим прямую 2x1 + x2 = 2. Изобразим ее график по двум точкам: (0;2) и (1;0). Наша прямая делит плоскость на две полуплоскости. При определении разрешенной полуплоскости, относительно граничной прямой, в анализируемое строгое неравенство 2x1 + x2 > 2 можно подставить координаты любой пробной точки (обычно, берут начало координат О (0;0)). Если координаты точки удовлетворяют этому неравенству, то вся полуплоскость, где лежит эта точка, является решением этого неравенства. Если нет, то решением этого неравенства является другая полуплоскость. Т. к. точка (0;0) не удовлетворяет неравенству 2x1 + x2 > 2, то разрешенная полуплоскость будет правее – выше граничной прямой 2x1 + x2 = 2. Аналогично поступаем для других ограничений. Неравенство (2) определяет разрешенную полуплоскость, расположенную на граничной прямой x1 + 3x2 = 3 (прямая строится по точкам (0;1) и (3;0)) и правее – выше нее, где x1 + 3x2 > 3 (что определяется пробной точкой (0;0)). Неравенство (3) определяет разрешенную полуплоскость, расположенную на граничной прямой x1 - x2 = -1 (прямая строится по точкам (0;1) и (-1;0)) и правее – ниже нее, где x1 - x2 > -1 (что определяется пробной точкой (0;0)). Неравенство (4) определяет разрешенную полуплоскость, расположенную на граничной прямой 3 x1 - x2 = 6 (прямая строится по точкам (0;-6) и (2;0)) и левее нее, где 3 x1 - x2 < 6 (что определяется пробной точкой (0;0)). Неравенство (5) определяет разрешенную полуплоскость, расположенную на граничной прямой x1 + x2 = 5 (прямая строится по точкам (0;5) и (5;0)) и левее – ниже нее, где x1 + x2 < 5 (что определяется пробной точкой (0;0)). Выражение (6) разрешает выбирать точки на прямой x1 = 0 (ось X2 в системе координат) и правее нее, где x1 > 0. Выражение (7) разрешает выбирать точки на прямой x2 = 0 (ось X1 в системе координат) и выше нее, где x2 > 0.
3. Общая часть всех разрешенных полуплоскостей (их пересечение) образует область допустимых решений (ОДР) решаемой задачи – это многоугольник АВСДЕ, координаты точек которого удовлетворяют условию неотрицательности переменных и неравенствам системы ограничений задачи.
4. Строим вектор N(c1; с2) = N(1; 2).
5. Целевая функция (8) геометрически представляет бесчисленное множество параллельных прямых. Для выделения одной из них приравняем многочлен (8) удобному для анализа произвольному числу, например нулю: F(x) = x1 + 2x2 = 0. Изобразим прямую
F(x) = x1 + 2x2 = 0 на графике по двум точкам: (0; 0) и (2; -1).
6. При увеличении целевой функции происходит графический параллельный перенос линии F(x) = 0 по направлению градиента вектора N(1; 2). Наибольшее значение целевая функция достигнет
в крайнем положении (на границе) множества допустимых решений.
На рис. 1 – это точка А: F(A) = Fmax. Координаты точки А являются решением задачи.
7. Найдем координаты точки А. Точка А - точка пересечения прямых L(3) и L(5), поэтому ее координаты найдем из системы уравнений:
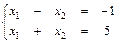
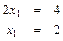
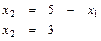
Отсюда имеем: А(2; 3), а Fmax = 2 + 2*3 = 8.
Линия уровня F(x) = 0 встретит многоугольник решений в точке D и в ней F(x) = Fmin. Можно найти координаты точки D (пересечение прямых L(1) и L(2)) из решения системы уравнений:
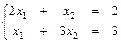
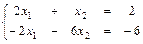
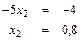
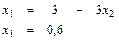
Отсюда D(0,6; 0,8), а Fmin = 0,6 + 0,8*2 = 2,2.
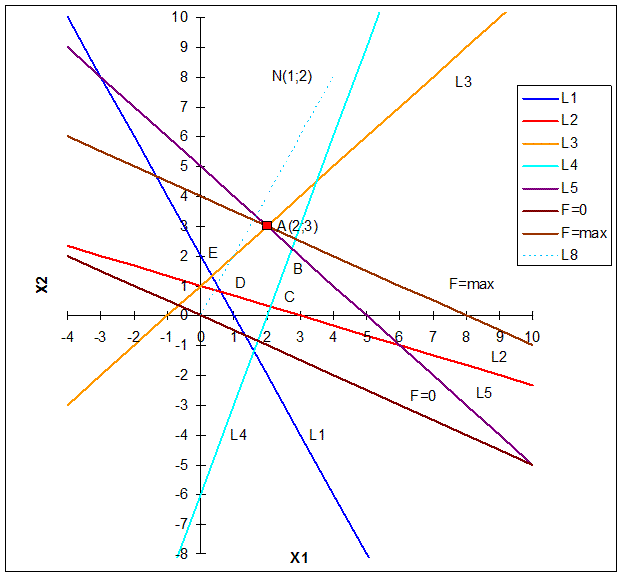
Рисунок 1. Графический метод решения задачи (задача 1).
 2020-05-21
2020-05-21 123
123







