Задача 2. Предприятие может производить два вида изделий А и В, располагая для их изготовления ограниченными ресурсами материала чугуна и стали соответственно в количестве 350 и 392 кг и оборудования в количестве 408 станко-часов. Данные, представленные в таблице, характеризуют затраты каждого из перечисленных трех видов ресурсов на изготовление одного вида изделия А и В.
Требуется определить сколько изделий А и В должно производить предприятие, чтобы достичь наибольшей прибыли.
Таблица 1.
| Виды ресурсов | Объем ресурсов (кг) | Затраты на одно изделие (кг) | |
| А | В | ||
| Чугун | 350 | 14 | 5 |
| Сталь | 392 | 14 | 8 |
| Оборудование | 408 | 6 | 12 |
| Прибыль в руб. | 10 | 5 | |
Введем искомые неизвестные: x1 – число изделий А; x2 – число изделий В; – которые должно производить предприятие (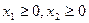 ).
).
Математически задачу можно сформулировать следующим образом: среди множества неотрицательных решений системы неравенств:
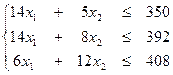 (1)
(1)
найти такое решение, для которого функция Z = 10x1 + 5x2 – достигает наибольшего значения.
 2020-05-21
2020-05-21 161
161







