Тема урока «Основные табличные интегралы. Непосредственное интегрирование.»
Цель урока. Показать учащимся принцип вывода формул интегрирования и применения их для нахождения интегралов методом непосредственного интегрирования.
Продолжать совершенствовать умения анализировать и обобщать полученные знания, подчеркивая, что основные формулы интегрирования дают возможность решать разнообразнейшие задачи с помощью простого алгоритма чисто алгебраического характера.
Вид занятия. Усвоение новых знаний.
План занятия.
Проверка домашнего задания.
Решить примеры из домашнего задания.
Фронтальный опрос по вопросам.
- Дайте определение первообразной функции.
- Сколько первообразных может иметь данная функция.
- Дайте определение неопределенного интеграла.
-Самостоятельная работа Программированный опрос в двух вариантах
--------------------------------------------------------------------------------------
Самостоятельная работа по теме
«Первообразная. Вычисление первообразных
---------------------------------------------------------------------------------------
З а д а н и е О т в е т
| 1 Вариант 2 Вариант | 1 | 2 | 3 |
Найти первообразные функции:
 
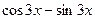  Первообразной функции
Первообразной функции  соответствует подынтегральная функция
соответствует подынтегральная функция 
 
| 


| 
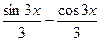
 
| 


|
Вариант - 2 1 3 2 вариант - 1 3 2
Задача. Для функции  найти ту первообразную, график которой проходит через точку
найти ту первообразную, график которой проходит через точку 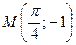 .
.
Решение: 




Задача. Точка движется по координатной прямой со скоростью
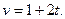 Найти закон движения, если известно, что в момент времени
Найти закон движения, если известно, что в момент времени  координата точки равнялась
координата точки равнялась 
Решение: 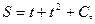
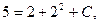


Изучение нового материала.
Составить таблицу основных формул интегрирования, проверяя ее дифференцированием правой части, то есть 



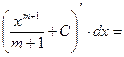



Примеры. Найти интегралы и проверить результат дифференцированием.




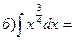













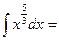
















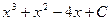

















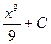











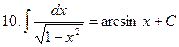






Все интегралы мы решали методом непосредственного интегрирования, то есть это метод основанный на использовании таблицы и основных свойств неопределенных интегралов. При этом возможны случаи:
а) данный интеграл сразу находится по таблице;
б) данный интеграл после применения свойств приводится к табличным;
в) данный интеграл после элементарных тождественных преобразований и применения свойств сводится к табличным.
Решить примеры.
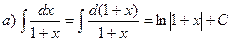







 2020-05-21
2020-05-21 74
74







