Литература
- Баврин, И.И. Высшая математика: учеб. для студ. естественно-научных спец. пед. вузов/ И.И. Баврин. - М.: Издательский центр «Академия»., 2004.– 616 с.
- Баврин, И.И. Математический анализ: учебник./ И.И. Баврин, М.: Высш. шк., 2006 – 327 с.
- Данко П. Е. Высшая математика в упражнениях и задачах: учеб. пособ. для вузов. В 2 ч. Ч. 1. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М.: Мир и Образование, 2003. – 304 с.
Теоретические положения
Опр. Пусть функция f определена на некотором промежутке, т.е. на отрезке, интервале или полуинтервале числовой оси. Функция F, определенная на этом же промежутке называется первообразной функции f, если выполнено (1.1) для каждого х из указанного промежутка.
Опр. Совокупность всех первообразных функции f, определенных на некотором промежутке <a,b>, называется неопределенным интегралом от функции f на этом промежутке и обозначается 
Основные свойства неопределенного интеграла
Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции.
 ,
, 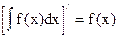 .
.
2. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого.
 .
.
Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла.
Ecли k = const, тогда
 .
.
Аддитивность интеграла относительно функций). Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме неопределенных интегралов от этих функций.
 .
.
Таблица простейших неопределенных интегралов
Обращая формулы дифференцирования, получим

| 
| |
| 1. |  , ,
|  ,(m¹-1); ,(m¹-1);
|
| 2. |  , ,
| 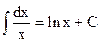 ,(x¹0); ,(x¹0);
|
| 3. |  , ,
|  ; ;
|
| 4. |  , ,
|  ,(a>0,a¹1); ,(a>0,a¹1);
|
| 5. |  , ,
| 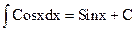 ; ;
|
| 6. |  , ,
|  ; ;
|
| 7. |  , ,
|  ; ;
|
| 8. | 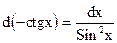 , ,
| 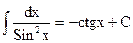 ; ;
|
| 9. |  , ,
| |
| 10. |  , ,
| 
|
| 11. |  , ,
| |
| 12. | 
| 
|
1 Метод замены переменной
Пусть нужно найти неопределенный интеграл от непрерывной функции 
Если обозначить  , то справедлива формула:
, то справедлива формула:
 .
.
Пример 1.
 .
.
Пример 2.

Пример 3.
 .
.
2 Интегрирование по частям
Формула интегрирования по частям имеет вид:
 .
.
Можно выделить два класса интегралов, для которых применима эта формула:
I.  II.
II.  .
.
В первом случае  , остаток
, остаток  , во втором случае, наоборот, первый сомножитель обозначают
, во втором случае, наоборот, первый сомножитель обозначают  , а остаток
, а остаток  где
где  – многочлен постоянной степени от
– многочлен постоянной степени от  .
.
Пример 4.
 Формула интегрирования по частям хорошо срабатывает и в других случаях.
Формула интегрирования по частям хорошо срабатывает и в других случаях.
Пример 5.


Перенесем все интегралы в левую часть. Получим:



Задания для занятия
Вычислите неопределенные интегралы
1.1. 
| 1.21. 
|
1.2. 
| 1.22. 
|
1.3. 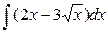
| 1.23. 
|
1.4. 
| 1.24. 
|
1.5. 
| 1.25. 
|
1.6. 
| 1.26. 
|
1.7. 
| 1.27. 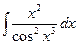
|
1.8. 
| 1.28. 
|
1.9. 
| 1.29. 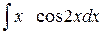
|
1.10. 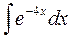
| 1.30. 
|
1.11. 
| 1.31. 
|
1.12. 
| 1.32. 
|
1.13. 
| 1.33. 
|
1.14. 
| 1.34. 
|
1.15. 
| 1.35. 
|
1.16. 
| 1.36. 
|
1.17.  
| 1.37. 
|
1.18. 
| 1.38. 
|
1.19. 
| 1.39. 
|
1.20. 
|
 2020-05-21
2020-05-21 154
154







