Определение 2.5.1. Праволинейная грамматика в нормальной форме (автоматная грамматика, регулярная грамматика, finite -state grammar) - это праволинейная грамматика, в которой каждое правило имеет вид  ,
,  , или
, или  , где
, где 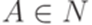 ,
, 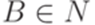 ,
,  .
.
Теорема 2.5.2. Каждая праволинейная грамматика эквивалентна некоторой праволинейной грамматике в нормальной форме.
Доказательство. Применим последовательно теорему 2.4.3, лемму 2.3.3 и воспользуемся конструкцией из доказательства теоремы 2.4.1.
Теорема 2.5.3. Если праволинейный язык не содержит пустого слова, то он порождается некоторой праволинейной грамматикой в нормальной форме без  -правил.
-правил.
Детерминированные конечные автоматы
Определение 2.6.1. Конечный автомат 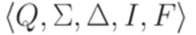 называется детерминированным (deterministic), если
называется детерминированным (deterministic), если
1. множество I содержит ровно один элемент;
2. для каждого перехода  выполняется равенство |x| = 1;
выполняется равенство |x| = 1;
3. для любого символа 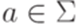 и для любого состояния
и для любого состояния  существует не более одного состояния
существует не более одного состояния  со свойством
со свойством  .
.
Пример 2.6.2. Конечный автомат из примера 2.1.14 является детерминированным.
Определение 2.6.3. Детерминированный конечный автомат  называется полным (complete), если для каждого состояния
называется полным (complete), если для каждого состояния  и для каждого символа
и для каждого символа  найдется такое состояние
найдется такое состояние  , что
, что  .
.
Пример 2.6.4. Конечный автомат из примера 2.1.14 эквивалентен полному детерминированному конечному автомату 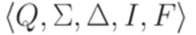 , где Q = {1,2,3},
, где Q = {1,2,3},  , I = {1}, F = {1,2},
, I = {1}, F = {1,2},


Замечание 2.6.5. Некоторые авторы используют в определении полного детерминированного конечного автомата вместо отношения  функцию
функцию  . От функции
. От функции 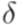 можно перейти к отношению
можно перейти к отношению  , положив
, положив
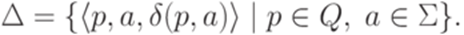
 2020-05-25
2020-05-25 259
259








