Свойства замкнутости класса автоматных языков

Теорема 3.1.1. Класс автоматных языков замкнут относительно итерации, конкатенации и объединения.

Доказательство. Без ограничения общности можно предположить, что каждый из исходных языков задан конечным автоматом с одним начальным и одним заключительным состоянием. Тогда во всех трех случаях результирующий автомат получается из исходных путем добавления нескольких -переходов и состояний и назначения новых начальных и заключительных состояний.

Пример 3.1.2. Пусть 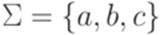. Рассмотрим конечный автомат

где

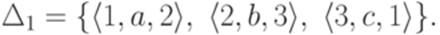
Тогда язык L(M₁)^* распознается конечным автоматом .

Пример 3.1.3. Пусть 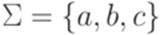. Рассмотрим конечный автомат M₁ из примера 3.1.2 и конечный автомат

где

Тогда язык распознается конечным автоматом

а язык распознается конечным автоматом

Пересечение и дополнение автоматных языков

Теорема 3.2.1. Класс автоматных языков замкнут относительно дополнения и пересечения.

Доказательство. Если язык L распознается полным детерминированным конечным автоматом 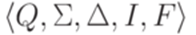, то язык распознается конечным автоматом .

Пересечение выражается через объединение и дополнение (закон де Моргана).

Замечание 3.2.2. Автоматность пересечения двух автоматных языков можно легко доказать и без привлечения теоремы 2.7.1. Для этого достаточно построить по двум конечным автоматам с однобуквенными переходами

новый конечный автомат

где