Пример 3.4.1. Рассмотрим язык 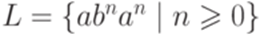 над алфавитом
над алфавитом  . Утверждение леммы 3.3.1 не выполняется ни для какого натурального числа p. Действительно, если w = abpap, то x = abk, y = bm, z = bp-k-map для некоторых
. Утверждение леммы 3.3.1 не выполняется ни для какого натурального числа p. Действительно, если w = abpap, то x = abk, y = bm, z = bp-k-map для некоторых 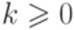 и
и 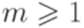 или
или  , y = abl, z = bp-lap для некоторого
, y = abl, z = bp-lap для некоторого 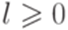 . В обоих случаях
. В обоих случаях 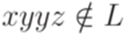 . Таким образом, язык L не является автоматным.
. Таким образом, язык L не является автоматным.
Замечание 3.4.3. Условие, сформулированное в лемме 3.3.1, является необходимым для автоматности, но не достаточным.
Пример 3.4.4. Пусть 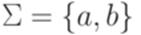 . Рассмотрим язык L = {akbman | k=0 или m=n}. Положим p = 1. Тогда для любого слова
. Рассмотрим язык L = {akbman | k=0 или m=n}. Положим p = 1. Тогда для любого слова 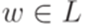 длины не меньше p найдутся слова
длины не меньше p найдутся слова 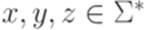 , соответствующие утверждению леммы 3.3.1. Тем не менее язык L не является автоматным, так как
, соответствующие утверждению леммы 3.3.1. Тем не менее язык L не является автоматным, так как
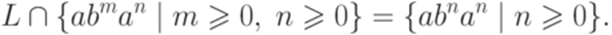
Лемма 3.4.5*. Пусть L - автоматный язык над алфавитом 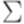 . Тогда найдется такое положительное целое число p, что для любого слова
. Тогда найдется такое положительное целое число p, что для любого слова 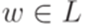 можно подобрать слова
можно подобрать слова 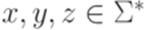 , для которых верно xyz = w,
, для которых верно xyz = w, 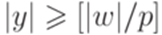 и
и 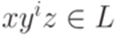 для всех
для всех 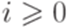 . Здесь [m] означает целую часть числа m.
. Здесь [m] означает целую часть числа m.
Доказательство. Пусть L распознается конечным автоматом 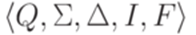 , содержащим только переходы с метками длины единица. Положим p = |Q|. Пусть слово w является меткой успешного пути
, содержащим только переходы с метками длины единица. Положим p = |Q|. Пусть слово w является меткой успешного пути 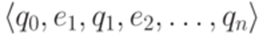 . Обозначим l = [|w|/p]. Если l = 0, то положим
. Обозначим l = [|w|/p]. Если l = 0, то положим  и
и  . Пусть
. Пусть 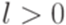 . Согласно принципу Дирихле найдутся такие натуральные числа j и k, что
. Согласно принципу Дирихле найдутся такие натуральные числа j и k, что 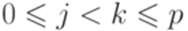 и qjl = qkl. Выберем слова x, y и z так, что |x| = jl, |y| = kl - jl и xyz = w.
и qjl = qkl. Выберем слова x, y и z так, что |x| = jl, |y| = kl - jl и xyz = w.
Эта лекция содержит дополнительные результаты, не используемые в дальнейшем изложении. В начале лекции доказывается замкнутость класса всех автоматных языков относительно взятия гомоморфного образа и относительно взятия полного гомоморфного прообраза.
В разделе 4.2* определяются понятия побуквенного гомоморфизма и локального языка и доказывается еще один критерий автоматности: среди языков, не содержащих пустого слова, автоматными являются в точности образы локальных языков при побуквенных гомоморфизмах.
В последнем разделе этой лекции устанавливается числовой критерий автоматности для языков над однобуквенным алфавитом (в терминах арифметических прогрессий) и доказывается связанное с длинами слов необходимое условие автоматности (для произвольного алфавита).
 2020-05-25
2020-05-25 251
251








