2020-05-25
140
Определение 5.1.1. Регулярное выражение над алфавитом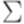 
определяется рекурсивно следующим образом: 0 является регулярным выражением; 1 является регулярным выражением; если 
, то a является регулярным выражением; если e и f являются регулярными выражениями, то 
, 
и 
тоже являются регулярными выражениями.
Для экономии скобок будем считать, что операция * связывает сильнее (то есть имеет более высокий приоритет), чем умножение, а умножение связывает сильнее, чем сложение. Вместо 
часто пишут просто 
.
Пример 5.1.2. Пусть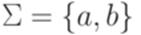 
. Тогда 
является регулярным выражением над алфавитом .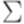
Определение 5.1.3. Каждое регулярное выражение e над алфавитом 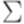задает (denotes, represents) некоторый язык над алфавитом 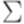(обозначение 
), определяемое рекурсивно следующим образом:
Заметим, что в правой части последнего выражения символом * обозначена итерация языка (см. определение 1.2.7).
Вместо 
часто пишут просто e.
Пример 5.1.4. Пусть 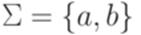. Согласно определению
Определение 5.1.5. Язык L называется регулярным если он задается некоторым регулярным выражением.
Определение 5.1.6. Пусть e - регулярное выражение. Тогда 
.
5.2*. Свойства регулярных выражений
Лемма 5.2.1. Регулярные выражения образуют ассоциативное полукольцо с операциями 
, то есть для любых регулярных выражений e, f и g выполняются следующие тождества:
1. e+f = f+e;
2. e+0 = e;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
10. 
.
Равенство понимается как равенство языков, задаваемых регулярными выражениями.
Лемма 5.2.2. Для любых регулярных выражений e и f выполняются следующие тождества:
1. e+e = e;
2. (1+e+ee+...+en-1)(en)* = e* для любого 
;
3. (e*f)*e* = (e+f)*;
4. 1+e(fe)*f = (ef)*.
Лемма 5.2.3. Для любых регулярных выражений e, f и g, если e = ef+g и 
, то e = gf*.
Теорема Клини
Определение 5.3.1. Назовем обобщенным конечным автоматом аналог конечного автомата, где переходы помечены не словами, а регулярными выражениями. Метка пути такого автомата - произведение регулярных выражений на переходах данного пути. Слово w допускается обобщенным конечным автоматом, если оно принадлежит языку, задаваемому меткой некоторого успешного пути.
Замечание 5.3.2. Каждый конечный автомат можно преобразовать в обобщенный конечный автомат, допускающий те же слова. Для этого достаточно заменить всюду в метках переходов пустое слово на 1, а каждое непустое слово - на произведение его букв.
Замечание 5.3.3. Если к обобщенному конечному автомату добавить переход с меткой 0, то множество допускаемых этим автоматом слов не изменится.
Пример 5.3.4. Пусть 
. Обобщенный конечный автомат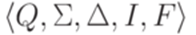 
, где Q = {1,2,3}, I = {1,2}, F = {3},
допускает все слова в алфавите 
, кроме слов, содержащих подслово aa.
Теорема 5.3.5 (теорема Клини). Язык L является регулярным тогда и только тогда, когда он является автоматным.
Доказательство. Пусть e - регулярное выражение. Индукцией по построению e легко показать, что задаваемый им язык является автоматным (см. теорему 3.1.1).
Обратно, пусть язык L распознается некоторым (недетерминированным) конечным автоматом с одним начальным состоянием и одним заключительным состоянием. Существует эквивалентный ему обобщенный конечный автомат 
, где 
. Если есть несколько переходов с общим началом и общим концом (такие переходы называются параллельными), заменим их на один переход, используя операцию +.
Устраним по очереди все состояния, кроме q1 и q2. При устранении состояния q нужно для каждого перехода вида 
, где 
, и для каждого перехода вида 
, где 
, добавить переход 
, где регулярное выражение g - метка перехода из q в q (если нет перехода из q в q, то надо добавить переход 
), и снова всюду заменить параллельные переходы на один переход, используя операцию +.
После устранения всех состояний, кроме q1 и q2, получится обобщенный конечный автомат 
, где
Очевидно, что 
.
Пример 5.3.6. Рассмотрим язык, распознаваемый конечным автоматом
где 
и
Тот же язык порождается обобщенным конечным автоматом
где
После устранения состояния q3 получается обобщенный конечный автомат
где
Можно упростить регулярные выражения и получить
После устранения состояния q4 и упрощения регулярных выражений получается обобщенный конечный автомат
где
Следовательно, язык L(M) задается регулярным выражением
Упростив это регулярное выражение, получим
5.4*. Звездная высота
Определение 5.4.1. Звездная высота (star-height) регулярного выражения (обозначение sh(e)) определяется рекурсивно следующим образом:
Пример 5.4.2. Пусть . Тогда
Определение 5.4.3. Звездной высотой регулярного языка L (обозначение sh(L)) называется минимум звездных высот регулярных выражений, задающих этот язык.
Замечание 5.4.4. Регулярный язык L является конечным тогда и только тогда, когда sh(L) = 0.
Теорема 5.4.5. Пусть 
. Тогда для любого 
существует такой регулярный язык 
, что sh(L) = n.
Доказательство можно найти в книге Саломаа А. Жемчужины теории формальных языков. - М.: Мир, 1986 с.41-46.
Пример 5.4.6. Пусть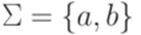 
и
Тогда sh(L) = 2. Действительно, язык L задается регулярным выражением (ab+ba+(aa+bb)(ab+ba)*(aa+bb))* и не задается никаким регулярным выражением меньшей звездной высоты.
Замечание 5.4.7. Неизвестно, верен ли аналог теоремы 5.4.5 для обобщенных регулярных выражений, в которых, помимо итерации, конкатенации и объединения, разрешена операция дополнения.
Основная цель данной лекции - доказать еще один критерий автоматности формального языка. Этот критерий можно сформулировать в терминах классов эквивалентности слов по взаимозаменяемости (однако формальные определения будут даны без использования понятия класса эквивалентности). Слова x и y считаются взаимозаменяемыми (относительно языка L), если при замене в любом слове из языка L подслова, совпадающего с x, на y снова получится слово из языка L и наоборот. В разделе 6.3 фактически доказывается, что язык L является автоматным тогда и только тогда, когда соответствующее отношение взаимозаменяемости разбивает множество всех слов рассматриваемого алфавита на конечное число классов эквивалентности.
Но сначала мы докажем аналогичный результат для отношения взаимозаменяемости не подслов, а префиксов (раздел 6.1). Соответствующие классы эквивалентности слов позволяют построить минимальный детерминированный конечный автомат для заданного языка. Известен и другой метод нахождения минимального детерминированного конечного автомата (раздел 6.2), но этот метод можно применять только тогда, когда уже имеется какой-нибудь детерминированный конечный автомат, распознающий данный язык. В конце лекции доказывается, что классы эквивалентности по взаимозаменяемости относительно автоматного языка сами являются автоматными языками.
