2020-05-21
136
Рассмотрим рисунок 7:
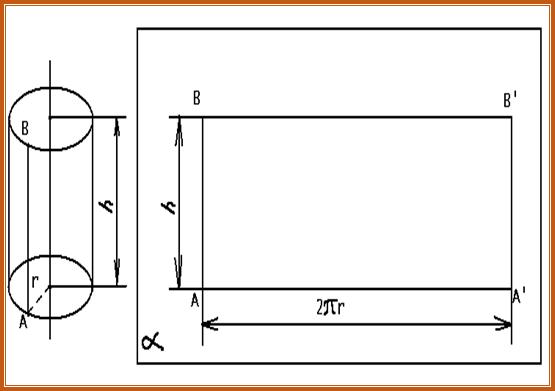
Представим себе, что боковую поверхность цилиндра разрезали по образующей AB и развернули таким образом, чтобы все образующие лежали в некоторой плоскости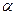 
. В результате в плоскости 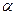получается прямоугольник 
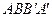. Этот прямоугольник называется разверткой боковой поверхности цилиндра. 
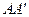– развертка окружности основания, поэтому 
. 
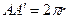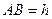– высота цилиндра.
За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Поэтому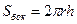 
.
Площадь полной поверхности равна: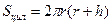 
.
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен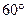 
. Найдите: а) высоту цилиндра; б) радиус цилиндра; в) площадь основания цилиндра.
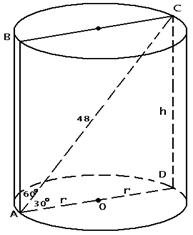
Дано:
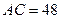
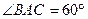
Найти:
а) h; б) r; в) Sосн
Решение:
а)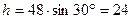 
б)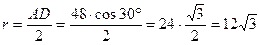 
в)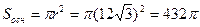 
.
№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3 см.
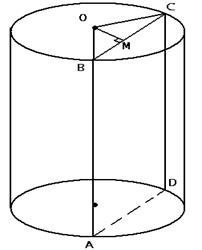
Дано:
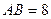
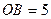
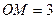
Найти:
SABCD
Решение:
.
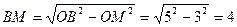
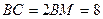
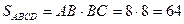Сегодня на уроке мы познакомились с новым телом в пространстве, выяснили из каких элементов оно состоит, рассмотрели различные его сечения, определили их развертку, научились вычислять площади его боковой и полной поверхностей.
На примерах решения задач посмотрели, как применять изученный материал к их решению. Научились строить чертежи цилиндра, его сечений и его развёртки.
Домашнее задание. Атанасян Л.С. Геометрия 10-11 п.59-60, п.77; №530, 538, 669.
