Дифференциальные уравнения первого порядка

1 2 3 4 5 6 7

Задача Коши

Общий вид дифференциального уравнения первого порядка:

Мы будем рассматривать уравнения, разрешенные относительно старшей производной, т.е. уравнения вида

. (2.1)

Часто рассматриваются также уравнения, которые удобно представлять несколько иначе:

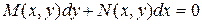. (2.2)

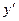Соответствие (2.2) с (2.1) таково: представляя правую часть (2.1) в виде дроби , а в левой заменяя на 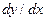и умножая (2.1) на и , получаем симметричную запись уравнения (2.1) в форме дифференциалов – уравнение (2.2).

Вообще, форма записи дифференциального уравнения в некоторых случаях подсказывает, как лучше исследовать его; нередко уравнение (2.1) бывает полезно представить и в таком виде

Если решение уравнения первого порядка зависит от одной-единственной произвольной постоянной: , то оно называется общим решением.

Если решение уравнения первого порядка представлено в неявной форме , где - произвольная постоянная, то соотношение называется общим интегралом.

Для дифференциального уравнения (2.1) задача Коши состоит в нахождении такого решения уравнения (2.1), которое принимает в заданной точке x₀ заданное значение 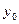, то есть

. (2.3)

Условие (2.3) называют начальным. Его часто записывают еще в такой форме .

Оказывается, что решение задачи Коши существует не всегда, и если существует, то не всегда единственно, что требует определенной осторожности при анализе полученных решений. Пусть, например, рассматривается задача Коши, описывающая какое-то физическое явление, и ее решение не единственно. Тогда найдя одно из решений, нельзя утверждать, что именно оно описывает рассматриваемое явление, а не какое-либо другое (не найденное нами!) решение той же задачи. Вот почему важна следующая теорема, называемая теоремой существования и единственности решения задачи Коши.

Теорема 2.1 (Коши). Если в уравнении (2.1) функция 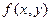и ее частная производная по переменной непрерывны в некоторой области на плоскости , содержащей некоторую точку , то существует единственное решение этого уравнения 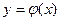, удовлетворяющее начальному условию (2.3): 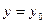при .В связи с теоремой 2.1 определение общего решения, данное выше, часто уточняют следующим образом: общим решением дифференциального уравнения первого порядка (2.1) называется такая функция , что

1) - решение уравнения (2.1) при любом значении C;

2) каково бы ни было начальное условие при (точка () берется из области, в которой решение соответствующей задачи Коши существует и единственно), можно найти такое значение , что функция удовлетворяет данному начальному условию.

Фиксируя значение , например с помощью начального условия, из общего решения дифференциального уравнения выделяем частное решение. Например, общим решением уравнения является (проверьте!). Начальное условие выделяет из общего решения частное .