Малые поперечные колебания мембраны описываются двумерным волновым уравнением, которое в цилиндрических координатах  имеет вид (см. 2.7.22):
имеет вид (см. 2.7.22):



 (7.5.1)
(7.5.1)
где  – амплитуда колебаний,
– амплитуда колебаний, 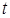 – время.
– время.

Рис. 7.5. К задаче о колебаниях мембраны.
В начальный момент времени  заданы начальное отклонение
заданы начальное отклонение  и начальная скорость
и начальная скорость  (рис. 7.5):
(рис. 7.5):


 (7.5.2)
(7.5.2)


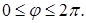 (7.5.3)
(7.5.3)
На границе  мембрана жестко закреплена, то есть на границе
мембрана жестко закреплена, то есть на границе 
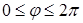 амплитуда колебаний равна нулю
амплитуда колебаний равна нулю


 (7.5.4)
(7.5.4)
Потребуем от искомого решения ограниченности в точке 


 (7.5.5)
(7.5.5)
и периодичности по углу  с периодом
с периодом 



 (7.5.6)
(7.5.6)
Таким образом, поставлена первая начально-краевая задача о малых колебаниях мембраны с неоднородными начальными условиями (7.5.2), (7.5.3) и однородным граничным условием первого рода (7.5.4).
Для решения этой задачи используем метод разделения переменных – пространственных  и времени
и времени 
 (7.5.7)
(7.5.7)
Подставляя (7.5.7) в (7.5.1) будем иметь равенство

разделив которое на  получим
получим
 (7.5.8)
(7.5.8)
где  – постоянная разделения; выбор ее знака обоснуем ниже.
– постоянная разделения; выбор ее знака обоснуем ниже.
Из (7.5.8) приходим к двум уравнениям: обыкновенному дифференциальному уравнению (ОДУ) относительно функции 
 (7.5.9)
(7.5.9)
и к уравнению в частных производных относительно 
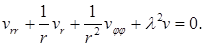 (7.5.10)
(7.5.10)
Подставим далее разделение переменных (7.5.7) в ограничения (7.5.4), (7.5.5), (7.5.6), приходим к следующим условиям для функции 

 (7.5.11)
(7.5.11)

 (7.5.12)
(7.5.12)


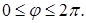 (7.5.13)
(7.5.13)
Задача (7.5.10)–(7.5.13) относительно функции  – задача на собственные функции
– задача на собственные функции  и собственные значения
и собственные значения  поскольку
поскольку 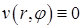 всегда является решением однородного уравнения (7.5.10) (это решение не приемлемо в силу представления решения в форме (7.5.7), так как
всегда является решением однородного уравнения (7.5.10) (это решение не приемлемо в силу представления решения в форме (7.5.7), так как  однако найдутся такие значения
однако найдутся такие значения  при которых
при которых  Таким образом, задача (7.5.10)–(7.5.13) – задача Штурма-Лиувилля на собственные значения
Таким образом, задача (7.5.10)–(7.5.13) – задача Штурма-Лиувилля на собственные значения  и собственные функции
и собственные функции  .
.
Будем решать задачу (7.5.10)–(7.5.13) также путем разделения переменных  и
и 
 (7.5.14)
(7.5.14)
Подставляя (7.5.14) в уравнение (7.5.10) будем иметь

или, деля на  и разделяя переменные, получим
и разделяя переменные, получим

где  – постоянная разделения.
– постоянная разделения.
Отсюда
 (7.5.15)
(7.5.15)
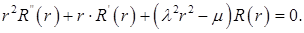 (7.5.16)
(7.5.16)
Подставляя далее (7.5.14) в (7.5.11)–(7.5.13), будем иметь
 (7.5.17)
(7.5.17)
 (7.5.18)
(7.5.18)
 (7.5.19)
(7.5.19)
Таким образом, пришли к задачам (7.5.15), (7.5.19) для отыскания функции  и (7.5.16)–(7.5.18) для функции
и (7.5.16)–(7.5.18) для функции 
Поскольку в задаче (7.5.15), (7.5.19) нас интересуют такие значения  , при которых существуют ненулевые ограниченные решения
, при которых существуют ненулевые ограниченные решения  в соответствии с (7.5.14), то задача (7.5.15), (7.5.19) – задача Штурма-Лиувилля на собственные значения
в соответствии с (7.5.14), то задача (7.5.15), (7.5.19) – задача Штурма-Лиувилля на собственные значения  и собственные функции
и собственные функции  – ограниченные для
– ограниченные для  и неограниченные для
и неограниченные для  так как при
так как при  фундаментальные решения уравнения (7.5.15) будут
фундаментальные решения уравнения (7.5.15) будут  и
и  а последнее неограничено при
а последнее неограничено при 
Фундаментальная система решений уравнения (7.5.15) для  с периодом
с периодом 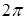 (см. (7.5.19)) будет
(см. (7.5.19)) будет

 (7.5.20)
(7.5.20)
и поскольку эти решения – периодические с периодом  то
то  может быть целым или нулем
может быть целым или нулем

 (7.5.21)
(7.5.21)
Таким образом, собственные значения  задачи (7.5.15), (7.5.19) определяются выражением
задачи (7.5.15), (7.5.19) определяются выражением

 , (7.5.22)
, (7.5.22)
а соответствующие им собственные функции имеют вид:
 (7.5.23)
(7.5.23)
Задача (7.5.16)–(7.5.18) с уже известными  является также задачей Штурма-Лиувилля, при решении которой требуется определить собственные значения
является также задачей Штурма-Лиувилля, при решении которой требуется определить собственные значения  и соответствующие им собственные функции
и соответствующие им собственные функции 
Уравнение (7.5.16) с  совпадает с уравнением (7.4.1) и заменой
совпадает с уравнением (7.4.1) и заменой  приводится к уравнению Бесселя
приводится к уравнению Бесселя 
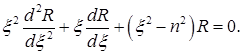 (7.5.24)
(7.5.24)
Общим решением уравнения (7.5.24) будет линейная комбинация функций Бесселя первого и второго рода порядка 
 (7.5.25)
(7.5.25)
Поскольку функция Неймана 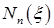 не ограничена при
не ограничена при  то в (7.5.25) на основании (7.5.18) полагаем
то в (7.5.25) на основании (7.5.18) полагаем 
В этом случае
 (7.5.26)
(7.5.26)
Подставляя (7.5.26) в граничное условие (7.5.17), получаем уравнение 
 (7.5.27)
(7.5.27)
определяющее собственные значения задачи (7.5.16)–(7.5.18)


 (7.5.28)
(7.5.28)
где  – корни функции Бесселя первого рода
– корни функции Бесселя первого рода  -го порядка
-го порядка 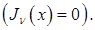
Собственные функции 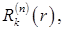 соответствующие собственным значениям (7.5.28), имеют вид
соответствующие собственным значениям (7.5.28), имеют вид


 (7.5.29)
(7.5.29)
В результате собственные функции задачи (7.5.10)–(7.5.13) в соответствии с (7.5.14) будут


 (7.5.30)
(7.5.30)
Таким образом, каждому собственному значению  соответствуют две собственные функции
соответствуют две собственные функции

 (7.5.31)
(7.5.31)
В рассмотренных ранее задачах каждому собственному значению соответствовала одна собственная функция. Кроме этого, если бы перед постоянной разделения в (7.5.8) был выбран знак «плюс», то вместо уравнения (7.5.27) мы получили бы уравнение  которое не имеет вещественных корней, так как модифицированная функция Бесселя
которое не имеет вещественных корней, так как модифицированная функция Бесселя  положительна на положительной полуоси
положительна на положительной полуоси  то есть график функции
то есть график функции  не пересекает оси абсцисс (см. рис. 7.3).
не пересекает оси абсцисс (см. рис. 7.3).
Перейдем к решению уравнения (7.5.9) с уже известными  тогда
тогда
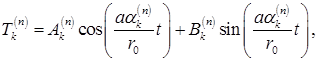

 (7.5.32)
(7.5.32)
В результате представления (7.5.7) решения уравнения (7.5.1) с учетом (7.5.31), (7.5.32) будут иметь вид:

 (7.5.33)
(7.5.33)
где  и
и  определяются равенствами (7.5.31).
определяются равенствами (7.5.31).
В силу линейности и однородности уравнения (7.5.1) сумма частных решений (7.5.33) по количеству собственных функций также будет решением, причем общим решением.

 (7.5.34)
(7.5.34)
Произвольные постоянные 


 определим путем подстановки (7.5.34) в начальные условия (7.5.2), (7.5.3) при
определим путем подстановки (7.5.34) в начальные условия (7.5.2), (7.5.3) при  получим
получим
 (7.5.35)
(7.5.35)
 (7.5.36)
(7.5.36)
Покажем, что функции  попарно ортогональны в круге
попарно ортогональны в круге 
 с весом
с весом  для различных значений
для различных значений 
 и
и 
 :
:
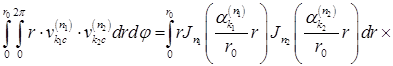

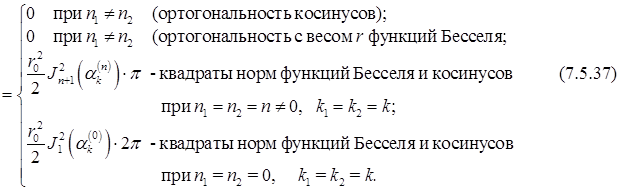
Аналогичный результат справедлив и для функций  то есть они также попарно ортогональны в круге
то есть они также попарно ортогональны в круге 
 и имеют ту же самую норму (5.7.37)
и имеют ту же самую норму (5.7.37)

 (7.5.38)
(7.5.38)
Легко убедиться в ортогональности функций  и
и  в круге
в круге 
 между собой. Действительно,
между собой. Действительно,

 (7.5.39)
(7.5.39)
так как функции  и
и  ортогональны на отрезке
ортогональны на отрезке  как при
как при  так и при
так и при 
Таким образом, выражения (7.5.35) и (7.5.36) представляют собой разложения в ряды известных функций 
 по ортогональным функциям.
по ортогональным функциям.
Учитывая это, умножим (7.5.35), (7.5.36) на  и проинтегрируем по кругу
и проинтегрируем по кругу 

 – произвольные натуральные числа), получим
– произвольные натуральные числа), получим


или переобозначая 
 получаем коэффициенты
получаем коэффициенты  и
и 


Учитывая (7.5.31) и (7.5.37), отсюда имеем
 (7.5.40)
(7.5.40)
 (7.5.41)
(7.5.41)
В (7.5.40), (7.5.41)  при
при  и
и  при
при 
Аналогично, умножая (7.5.35), (7.5.36) на  интегрируя по кругу
интегрируя по кругу 
 и переобозначая индексы
и переобозначая индексы 
 получим
получим
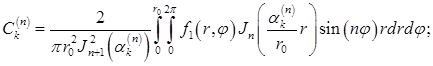 (7.5.42)
(7.5.42)
 (7.5.43)
(7.5.43)
В коэффициентах (7.5.40)–(7.5.43) 
 причем при
причем при 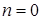
 для всех
для всех 
Итак, ряд (7.5.34) с коэффициентами (7.5.40)–(7.5.43) является решением задачи (7.5.1)–(7.5.6).
Полученное решение (7.5.34), (7.5.40)–(7.5.43) довольно громоздко, поэтому в заключение этого параграфа рассмотрим случай, когда функции 
 не зависят от
не зависят от  (осесимметричная задача).
(осесимметричная задача).

 (7.5.44)
(7.5.44)
Тогда в (7.5.40)–(7.5.43) появятся интегралы
 и
и  ,
, 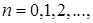
из которых лишь первый отличен от нуля и то при  (равен
(равен  ). Поэтому все коэффициенты
). Поэтому все коэффициенты

 (7.5.45)
(7.5.45)
Среди коэффициентов 
 отличны от нуля лишь коэффициенты при
отличны от нуля лишь коэффициенты при 
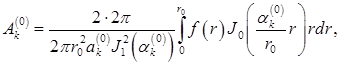 (7.5.46)
(7.5.46)
 (7.5.47)
(7.5.47)
Тогда ряд (7.5.34) с учетом (7.5.31) при  запишется так
запишется так
 (7.5.48)
(7.5.48)
Ряд (7.5.48) с коэффициентами (7.5.46), (7.5.47) – решение задачи (7.5.1)–(7.5.6) в случае когда 

 2020-05-25
2020-05-25 1740
1740