Пусть в круглом цилиндре высотой 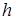 и радиусом
и радиусом  поддерживается стационарное температурное поле
поддерживается стационарное температурное поле 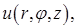 где
где  – цилиндрическая система координат. На основаниях цилиндра
– цилиндрическая система координат. На основаниях цилиндра  распределение температуры задано осесимметрично и одинаково (рис. 7.6)
распределение температуры задано осесимметрично и одинаково (рис. 7.6)
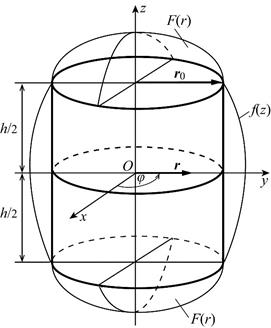
Рис. 7.6. К задаче теплопроводности в цилиндре конечных размеров.


 (7.6.1)
(7.6.1)
На боковой поверхности цилиндра распределение температур также задано осесимметрично и симметрично относительно плоскости 



 (7.6.2)
(7.6.2)
В условиях отсутствия источников стационарное распределение теплоты описывается уравнением Лапласа (2.2.1) (отсутствует производная по времени  ), которое в цилиндрической системе координат
), которое в цилиндрической системе координат  имеет вид (2.7.20):
имеет вид (2.7.20):
 (7.6.3)
(7.6.3)
Физически ясно, что поскольку распределение температуры на торцах и боковой поверхности цилиндра осесимметрично и симметрично относительно плоскости  , то оно будет обладать теми же свойствами и внутри цилиндра, то есть производная
, то оно будет обладать теми же свойствами и внутри цилиндра, то есть производная  тогда уравнение (7.6.3) для определения функции
тогда уравнение (7.6.3) для определения функции 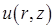 имеет вид:
имеет вид:


 (7.6.4)
(7.6.4)
На границах цилиндра заданы граничные условия (7.6.1), (7.6.2) в виде

 (7.6.5)
(7.6.5)


 (7.6.6)
(7.6.6)
а внутри цилиндра задаются условия четности


 (7.6.7)
(7.6.7)
Кроме этого, в точке  задается условие ограниченности функции
задается условие ограниченности функции 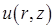

 (7.6.8)
(7.6.8)
Таким образом, поставлена первая краевая задача (7.6.4)–(7.6.8) для уравнения Лапласа в двумерной цилиндрической системе координат  для ограниченного цилиндра.
для ограниченного цилиндра.
Поскольку задача содержит неоднородные краевые условия, применим к ее решению метод редукции сведения к более простым задачам. С этой целью представим функцию 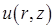 в виде суммы
в виде суммы
 (7.6.9)
(7.6.9)
Подставляя (7.6.9) в задачу (7.6.4)–(7.6.8), приходим к системе





из которой выделяется задача для функции  с однородным граничным условием на боковой поверхности цилиндра и неоднородным граничным условием на торцах (подчеркнута)
с однородным граничным условием на боковой поверхности цилиндра и неоднородным граничным условием на торцах (подчеркнута)


 (7.6.10)
(7.6.10)

 (7.6.11)
(7.6.11)

 (7.6.12)
(7.6.12)


 (7.6.13)
(7.6.13)

 (7.6.14)
(7.6.14)
и задача для функции  с неоднородным граничным условием на боковой поверхности цилиндра и неоднородным – на торцах (остальные члены)
с неоднородным граничным условием на боковой поверхности цилиндра и неоднородным – на торцах (остальные члены)


 (7.6.15)
(7.6.15)

 (7.6.16)
(7.6.16)

 (7.6.17)
(7.6.17)


 (7.6.18)
(7.6.18)

 (7.6.19)
(7.6.19)
Для решения задачи (7.6.10)–(7.6.14) используем метод разделения переменных
 (7.6.20)
(7.6.20)
Подставляя (7.6.20) в (7.6.10), приходим к равенству

деля которое на  получим
получим

где знак  обоснован ниже. Из последних равенств получаем следующие два обыкновенных дифференциальных уравнения (ОДУ)
обоснован ниже. Из последних равенств получаем следующие два обыкновенных дифференциальных уравнения (ОДУ)
 (7.6.21)
(7.6.21)
 (7.6.22)
(7.6.22)
Подставляя (7.6.20) в (7.6.12) (полагая  в противном случае тогда в (7.6.20)
в противном случае тогда в (7.6.20)  что не приемлемо), получим
что не приемлемо), получим
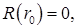 (7.6.23)
(7.6.23)
то есть получили граничное условие для ОДУ (7.6.22).
Второе граничное условие для этого ОДУ получим из условия ограниченности решения при  то есть из условия (7.6.14)
то есть из условия (7.6.14)
 (7.6.24)
(7.6.24)
Задача (7.6.22)–(7.6.24) всегда имеет нулевое решение, однако существуют такие  которым соответствуют ненулевые решения и следовательно задача (7.6.22)–(7.6.24) – задача на собственные значения
которым соответствуют ненулевые решения и следовательно задача (7.6.22)–(7.6.24) – задача на собственные значения  и собственные функции
и собственные функции  (задача Штурма-Лиувилля).
(задача Штурма-Лиувилля).
Перепишем уравнение (7.6.22) в форме

и сделав замену
 (7.6.25)
(7.6.25)
получим уравнение Бесселя
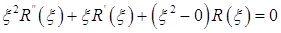 (7.6.26)
(7.6.26)
с нулевым индексом 
Общим решением его будет
 (7.6.27)
(7.6.27)
Поскольку функция Неймана  не ограничена при
не ограничена при  то в соответствии с условием ограниченности (7.6.24) полагаем в (7.6.27)
то в соответствии с условием ограниченности (7.6.24) полагаем в (7.6.27) 
Таким образом,
 (7.6.28)
(7.6.28)
где  – функция Бесселя первого рода нулевого порядка
– функция Бесселя первого рода нулевого порядка 
Подставляя (7.6.28) в граничное условие (7.6.23), получим
 (7.6.29)
(7.6.29)
Поскольку  (в противном случае
(в противном случае  и
и  из (7.6.20), что не приемлемо), то
из (7.6.20), что не приемлемо), то
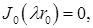 (7.6.30)
(7.6.30)
откуда получаем
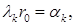

 (7.6.31)
(7.6.31)
где 
 – корни уравнения (7.6.30).
– корни уравнения (7.6.30).
Если бы при разделении переменных перед  был поставлен знак «плюс», то мы пришли бы вместо уравнения (7.6.30) к уравнению
был поставлен знак «плюс», то мы пришли бы вместо уравнения (7.6.30) к уравнению
 (7.6.32)
(7.6.32)
где  – модифицированная функция Бесселя нулевого порядка. Так как
– модифицированная функция Бесселя нулевого порядка. Так как  всюду на полуоси
всюду на полуоси  то график ее не пересекает оси абсцисс и следовательно корни отсутствуют.
то график ее не пересекает оси абсцисс и следовательно корни отсутствуют.
Таким образом, из (7.6.28) и (7.6.31) собственными функциями задачи (7.6.22)–(7.6.24), соответствующие собственным значениям (7.6.31) с точностью до постоянной, будут

 (7.6.33)
(7.6.33)
Уравнению (7.6.21) должно удовлетворять условие четности
 (7.6.34)
(7.6.34)
полученное подстановкой (7.6.20) в (7.6.13).
Общим решением уравнения (7.6.21) будет функция
 (7.6.35)
(7.6.35)
Поскольку функция 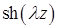 – нечетная
– нечетная  , то в (7.6.35)
, то в (7.6.35)
коэффициент  в соответствии с (7.6.34)полагаем равным нулю, то есть
в соответствии с (7.6.34)полагаем равным нулю, то есть

 (7.6.36)
(7.6.36)
Следовательно, на основе (7.6.33) и (7.6.36) решения (7.6.20) примут вид:

 (7.6.37)
(7.6.37)
Сумма решений (7.6.37) по количеству собственных функций снова является решением, то есть
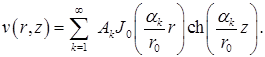 (7.6.38)
(7.6.38)
Коэффициенты  найдем, подставив (7.6.38) в краевое условие (7.6.11), тогда
найдем, подставив (7.6.38) в краевое условие (7.6.11), тогда
 (7.6.39)
(7.6.39)
то есть (7.6.39) – ряд Фурье-Бесселя функции  с коэффициентами
с коэффициентами 
Из (7.6.39), в соответствии с (7.4.14), (7.4.15), находим
 (7.6.40)
(7.6.40)
Таким образом, ряд (7.6.38) с коэффициентами (7.6.40) представляет решение задачи (7.6.10)–(7.6.14).
 2020-05-25
2020-05-25 1136
1136
