Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
sin2α+cos2α=1sin2α+cos2α=1
tgα=sinαcosα,ctgα=cosαsinαtgα=sinαcosα,ctgα=cosαsinα
tgα⋅ctgα=1tgα⋅ctgα=1
Зависимость между синусом и косинусом
sin2α+cos2α=1sin2α+cos2α=1
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
tgα=sinαcosα,ctgα=cosαsinαtgα=sinαcosα,ctgα=cosαsinα
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой yx=sinαcosαyx=sinαcosα, а отношение xy=cosαsinαxy=cosαsinα — будет являться котангенсом.
Добавим, что только для таких углов αα, при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества tgα=sinαcosαtgα=sinαcosα, ctgα=cosαsinαctgα=cosαsinα.
Например: tgα=sinαcosαtgα=sinαcosα является справедливой для углов αα, которые отличны от π2+πzπ2+πz, а ctgα=cosαsinαctgα=cosαsinα — для угла αα, отличного от πzπz, zz — является целым числом.
Зависимость между тангенсом и котангенсом
tgα⋅ctgα=1tgα⋅ctgα=1
Данное тождество справедливо только для таких углов αα, которые отличны от π2zπ2z. Иначе или котангенс или тангенс не будут определены.
Опираясь на вышеизложенные пункты, получаем, что tgα=yxtgα=yx, а ctgα=xyctgα=xy. Отсюда следует, что tgα⋅ctgα=yx⋅xy=1tgα⋅ctgα=yx⋅xy=1. Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.
Зависимости между тангенсом и косинусом, котангенсом и синусом
tg2α+1=1cos2αtg2α+1=1cos2α — сумма квадрата тангенса угла αα и αα, отличных от π2+πzπ2+πz.
1+ctg2α=1sin2α1+ctg2α=1sin2α — сумма αα, равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого αα, отличного от πzπz.
ТРИГОНОМЕТРИЯМАТЕМАТИКА ТРИГОНОМЕТРИЯ ФОРМУЛЫ ТЕОРИЯ
Найдите sinαsinα и tgαtgα, если cosα=−12cosα =−12 и π2<α<π π2<α<π;
Функции sinαsinα и cosαcosα связывает формула sin2α+cos2α=1sin2α+cos2α=1. Подставив в эту формулу cosα=−12cosα=−12, получим:
sin2α+(−12)2=1sin2α+(−12)2=1
Это уравнение имеет 2 решения:
sinα=±1−14−−−−−√=±3–√2sinα=±1−14=±32
По условию π2<α<ππ2<α<π. Во второй четверти синус положителен, поэтому sinα=3–√2sinα=32.
Для того, чтобы найти tgαtgα, воспользуемся формулой tgα=sinαcosαtgα=sinαcosα. Соответствующие величины нам известны.
tgα=3–√2:12=3–√tgα=32:12=3
уровень8 класспредметматематикасложностьпростая
Найдите cosαcosα и ctgαctgα, если sinα=3–√2sinα=32 и π2<α<ππ2<α<π.
Подставив в формулу sin2α+cos2α=1sin2α+cos2α=1 данное по условию число sinα=3–√2sinα=32, получаем (3–√2)2+cos2α=1(32)2+cos2α=1. Это уравнение имеет два решения cosα=±1−34−−−−−√=±14−−√cosα=±1−34=±14.
По условию π2<α<ππ2<α<π. Во второй четверти косинус отрицателен, поэтому cosα=−14−−√=−12cosα=−14=−12.
Для того, чтобы найти ctgαctgα, воспользуемся формулой ctgα=cosαsinαctgα=cosαsinα. Соответствующие величины нам известны.
ctgα=−12:3–√2=−13–√ctgα=−12:32=−13.
Любой угол измеряется либо в градусной мере измерения (единица измерения – градус) либо в радианной (единица измерения – радиан). Один дуговой градус – это 1 360 часть окружности. Один угловой градус – это центральный угол, опирающийся на дуговой градус. Радианная мера угла – это отношение длины дуги к радиусу этой дуги. Радиан – это центральный угол, опирающийся на дугу, равную длине радиуса этой дуги. Окружность содержит 2p радиан.
46p 9; 2) 5p 8; 4) 7p 12; 6) 11p 12; 8) 47p 9. Для произвольного угла Основные тригонометрические тождества O r O Rr O a Rr O A a Rr O 180 2,1 A p × = = 17 2
определенного радиуса, то любому центральному углу α окружности соответствует дуга AB. Зафиксируем такой центральный угол, для которого длина дуги AB будет равна радиусу
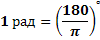
И наоборот
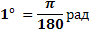
Так как π = 3,14, то 1 рад = 57,3°
Если угол содержит a радиан, то его градусная мера равна
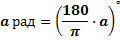
И наоборот
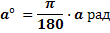
Обычно при обозначении меры угла в радианах наименование «рад» опускают.
Например, 360° = 2π рад, пишут 360° = 2π
В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.
| Градусы | 0 | 15 | 30 | 45 | 60 | 75 | 90 | 120 | 135 | 150 | 180 | 270 | 360 |
| Радианы | 0 | π/12 | π/6 | π/4 | π/3 | 5π/12 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 3π/2 | 2π |
Пример 1.
Найти радианную меру угла равного а) 40°, б)120°, в)105°
Решение
а) 40° = 40·π / 180 = 2π/9
б) 120° = 120·π/180 = 2π/3
в) 105° = 105·π/180 = 7π/12
Пример 2.
Найти градусную меру угла выраженного в радианах а) π/6, б) π/9, в) 2·π/3
Решение
а) π/6 = 180°/6 = 30°
б) π/9 = 180°/9 = 20°
в) 2π/3 = 2·180°/6 = 120°
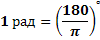
И наоборот
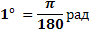
Так как π = 3,14, то 1 рад = 57,3°
Если угол содержит a радиан, то его градусная мера равна
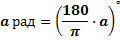
И наоборот
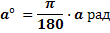
Обычно при обозначении меры угла в радианах наименование «рад» опускают.
Например, 360° = 2π рад, пишут 360° = 2π
В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.
| Градусы | 0 | 15 | 30 | 45 | 60 | 75 | 90 | 120 | 135 | 150 | 180 | 270 | 360 |
| Радианы | 0 | π/12 | π/6 | π/4 | π/3 | 5π/12 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 3π/2 | 2π |
Пример 1.
Найти радианную меру угла равного а) 40°, б)120°, в)105°
Решение
а) 40° = 40·π / 180 = 2π/9
б) 120° = 120·π/180 = 2π/3
в) 105° = 105·π/180 = 7π/12
Пример 2.
Найти градусную меру угла выраженного в радианах а) π/6, б) π/9, в) 2·π/3
Решение
а) π/6 = 180°/6 = 30°
б) π/9 = 180°/9 = 20°
в) 2π/3 = 2·180°/6 = 120°
Формулы сложения.
sin (α + β) = sin α · cos β + sin β · cos α
sin (α - β) = sin α · cos β - sin β · cos α
cos (α + β) = cos α · cos β - sin α · sin β
cos (α - β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
 2020-05-25
2020-05-25 137
137







