Формулы двойного угла

cos 2α = cos² α - sin² α

cos 2α = 2cos² α - 1

cos 2α = 1 - 2sin² α

sin 2α = 2sin α · cos α

tg 2α = (2tg α) ÷ (1 - tg² α)

ctg 2α = (ctg² α - 1) ÷ (2ctg α)

 

Формулы тройного угла.

sin 3α = 3sin α - 4sin³ α

cos 3α = 4cos³ α - 3cos α

tg 3α = (3tg α - tg³ α) ÷ (1 - 3tg² α)

ctg 3α = (3ctg α - ctg³ α) ÷ (1 - 3ctg² α)

 

Формулы половинного угла.

 

1. Синус половинного угла. Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол α/2 в левой части. Данное правило справедливо также для других формул, приведенных ниже.

2. Косинус половинного угла:

3. Тангенс половинного угла:

4. Котангенс половинного угла:

5. Выражение синуса через тангенс половинного угла:

6. Выражение косинуса через тангенс половинного угла:

7. Выражение тангенса через тангенс половинного угла:

8. Выражение котангенса через тангенс половинного угла:

9. Для выполнения тождественных преобразований необходимо знать следующие формулы:
1.Формулы сложения
.
2.Формулы двойного аргумента
.
3.Формулы половинного аргумента
.
4.Формулы понижения степени

10.

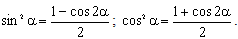
11. 5.Формулы преобразования суммы в произведения

12. 6.Формулы преобразования произведений в суммы
.
7. Определения обратных тригонометрических функций
.

13. 8. Тригонометрические уравнения
.

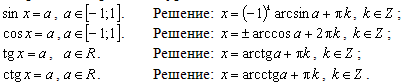Базовый уровень

15. Пример 1. Вычислить .

16. Решение:

17.

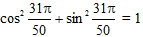
18. Ответ: 1.

19.

20. Пример 2. Найти значение sinα, если .

21. Решение:

22. Так как синус в IV четверти имеет отрицательное значение, то .

23. Ответ: – 0,6.

24.

25. Пример 3. Найти значение , если .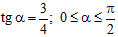

26. Решение:

27. Из формулы найдём . Так как α лежит в I четверти, то cosα положителен и .

28. Из формулы найдём .

29. .

30. Ответ: 7,2.

31.

32. Пример 4. Решите уравнение .

33. Решение:

34. .

35. Умножим левую и правую части равенства на 5 и, учитывая, что , получаем .

36. Ответ: .

37.

38. Пример 5. Вычислить .

39. Решение:

40. Согласно формулам сложения, имеем .

41. Ответ: 1.

42.

43. Пример 6. Приведите значение аргумента к I четверти: .

44. Решение:

45. По алгоритму формул приведения: .

46. Ответ: .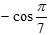

Повышенный уровень

48. Пример 7. Упростить .

49. Решение:

50.

51. Ответ: .

52.

53. Пример 8. Вычислить .

54. Решение:

55. Воспользуемся формулами преобразования произведений в сумму и формулами приведения, получим:

56.

57. .

58. Ответ: 1.

59.

60. Пример 9. Решите уравнение 3 ctgx-cos2x=1+2sin2x.

61. Решение:

62.

63. Уравнение

64. Уравнение 3-4sin²x-2cosx•sinx=0 3cos²x-sin²x-2cosx•sinx=0 – однородное уравнение второй степени, которое решается путём почленного деления на cos²x или sin²x . Разделим на cos²x: tg²x+2tgx-3=0 – уравнение второй степени. Путём подстановки tgx=t приводим его к алгебраическому квадратному: t²+2t-3=0, где t¹=-3; t₂=1.

65.

66.

67. При всех значениях x₁, x₂, x₃ .

68. Ответ: .