Определение неопределенного интеграла

Направление 08.03.01 «Строительство» Вопросы к экзамену по дисциплине «Математический анализ» (2 семестр)

Понятие первообразной функции, неопределенного интеграла.

Определение первообразной.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство формула для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство формула. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .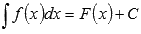

Выражение называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

1.
Производная результата интегрирования равна подынтегральной функции.

2.
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

3. , где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.

4.

2. Свойства неопределенного интеграла.

Свойства неопределенного интеграла	Формула
1. Неопределенный интеграл от дифференциала некоторой функции равен сумме самой этой функции и произвольной постоянной	∫dƒ(x) = ƒ(x)+C
2.Производная неопределенного интеграла равна подинтегральной функции	(∫ƒ(x)dx)' = ƒ(x)
3.Дифференциал неопределенного интеграла равен подинтегральному выражению	d∫ƒ(x)dx = ƒ(x)dx
4.Постоянный множитель можно выносить за знак интеграла	∫a·ƒ(x)dx = a∫ƒ(x)dx, причем a ≠ 0
5.Интеграл суммы (или разности) равен сумме (или разности) интегралов	∫[ƒ(x) ± g(x)]dx = ∫ƒ(x)dx ± ∫g(x)dx
6.Свойство является комбинацией свойств 4 и 5	∫[a·ƒ(x) ± b·g(x)]dx = a·∫ƒ(x)dx ± b·∫g(x)dx, причем a ≠ 0 ^ b ≠ 0
7.Свойство инвариантности неопределенного интеграла	Если ∫ƒ(x)dx = F(x)dx, то ∫ƒ(u(x))du(x) = F(u(x))+C

 

Таблица интегралов.

 

 

4. Метод замены переменной.

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Например:

      У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.

     Заменим выражение  буквой t

Получилось обычное квадратное уравнение! Решив его, найдем чему равно t, после чего, сделав обратную замену, вычислим x.

5.Метод внесения под знак дифференциала функции.

При сведении заданного интеграла к табличному часто используются следующие преобразования дифференциала как операция «подведения под знак дифференциала». При этом используется формула:

Вообще говоря, внесение (подведение) под знак дифференциала и замена переменной (метод подстановки) – это один и тот же метод нахождения неопределенного интеграла; отличие состоит только в оформлении.

Суть метода

Итак, внесение под знак интеграла опирается на следующее правило интегрирования. Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала, то

 

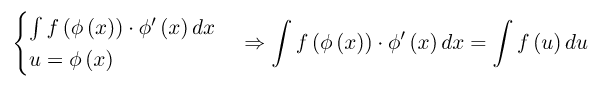
6. Метод интегрирования по частям.

7. Интегрирование рациональных дробей.

8. Метод неопределенных коэффициентов.

9. Метод интегрирования иррациональности вида .

10. Метод интегрирования иррациональности вида

11. Метод интегрирования иррациональности вида

12. Интегрирование тригонометрических выражений вида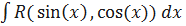

13. Задачи, о площади криволинейной трапеции.

14. Понятие интегральной суммы. Геометрический смысл интегральной суммы.

15. Понятие определенного интеграла. Геометрический смысл определенного интеграла.

16. Свойства определенного интеграла. Формула Ньютона-Лейбница.

17. Метод замены переменной в определенном интеграле.

18. Метод интегрирования по частям в определенном интеграле.

19. Вычисление площадей плоских фигур.

20. Вычисление объема тела вращения.

21. Вычисление дуги кривой.

22. Вычисление площади поверхности вращения.

23. Основные понятия дифференциальных уравнений.

24. Неполные дифференциальные уравнения 1 порядка. Дифференциальные уравнения с разделяющимися переменными.

25. Однородные дифференциальные уравнения 1 порядка.

26. Линейные дифференциальные уравнения 1 порядка. Способ решения.

27. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка.

28. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

29. Понятие числового ряда. Частичная сумма числового ряда. Понятие сходящегося ряда.

30. Свойства сходящихся рядов.

31. Необходимый признак сходимости ряда. Гармонический ряд.

32. Признак сходимости рядов с положительными членами. Сравнение рядов с положительными членами.

33. ''Эталонные ряды'', используемые для сравнения.

34. Признак Даламбера и Коши. Интегральный признак сходимости.

35. Понятие знакочередующегося ряда. Признак Лейбница.

36. Понятие знакопеременного ряда. Достаточный признак сходимости знакопеременного ряда.

37. Понятие абсолютно сходящегося ряда. Понятие условно сходящегося ряда.

38. Понятие степенного ряда. Область сходимости степенного ряда. Теорема Абеля.

39. Радиус сходимости степенного ряда. Формула Даламбера и Коши.

40. Свойства степенных рядов. Непрерывность, интегрируемость и дифференцируемость степенных рядов.

41. Ряд Маклорена.

42. Разложение в ряд Маклорена функции  y =  

43. Разложение в ряд Маклорена функции y = sin(x).

44. Разложение в ряд Маклорена функции y = cos(x).

45. Разложение в ряд Маклорена функции m y = .

46. Разложение в ряд Маклорена функции y = ln(1+ x).

47. Разложение в ряд Маклорена функции y = arctg(x).

48. Формула Тейлора. Остаточный член формулы Тейлора.