В общем случае преобразуемая неэлектрическая величина является функцией времени 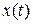 . ИП не должен искажать эту зависимость, и между входным и выходным параметрами должно сохраняться уравнение преобразования
. ИП не должен искажать эту зависимость, и между входным и выходным параметрами должно сохраняться уравнение преобразования 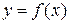 в виде
в виде 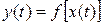 .
.
Для ИП с линейной характеристикой (см. зависимости 1 и 2 на рис. 1.2) это уравнение принимает вид
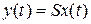 ,
,
где S – чувствительность ИП.
Последнее уравнение характерно для некоторого идеального безынерционного ИП, каких практически не бывает. Реальный ИП всегда имеет определенную инерционность, зависящую от конструкции и типа ИП: наличия движущихся частей, емкостных и индуктивных элементов, нелинейных элементов, помех.
Для оценки качества работы ИП в динамическом режиме рассмотрим его динамические характеристики, которые делят на полные и частные.
С помощью полных динамических характеристик можно восстановить входной преобразуемый сигнал по полученному выходному параметру ИП.
С помощью частных динамических характеристик восстановить входной сигнал по полученному выходному параметру невозможно.
К полным динамическим характеристикам относится прежде всего дифференциальное уравнение, связывающее величины 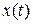 и
и 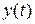 :
: 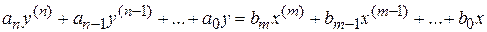 , где индексы при y и x означают порядок дифференцирования по времени. Порядок дифференциального уравнения может быть различным и зависит от структуры ИП. Вид решения дифференциального уравнения определяется характером изменения входного сигнала. Например, при синусоидальном входном сигнале
, где индексы при y и x означают порядок дифференцирования по времени. Порядок дифференциального уравнения может быть различным и зависит от структуры ИП. Вид решения дифференциального уравнения определяется характером изменения входного сигнала. Например, при синусоидальном входном сигнале 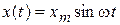 выходная величина
выходная величина 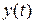 также имеет синусоидальный характер изменения с комплексной амплитудой
также имеет синусоидальный характер изменения с комплексной амплитудой 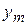 , сдвинутой на угол
, сдвинутой на угол 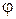 по отношению к
по отношению к 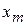 .
.
Существует понятие динамической чувствительности, являющейся отношением комплексного значения выходного сигнала к комплексному значению входного: 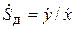 . В случае синусоидального входного сигнала
. В случае синусоидального входного сигнала 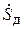 представляет собой комплексную величину, зависящую от частоты изменения
представляет собой комплексную величину, зависящую от частоты изменения 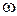 входного сигнала. Динамическая чувствительность в комплексном виде представляется выражением
входного сигнала. Динамическая чувствительность в комплексном виде представляется выражением
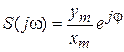 .
.
При этом выходная величина описывается вектором 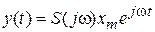 с действительной частью
с действительной частью 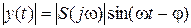 . Модуль комплексной чувствительности и угол сдвига между входной и выходной величинами являются функциями частоты. Зависимости
. Модуль комплексной чувствительности и угол сдвига между входной и выходной величинами являются функциями частоты. Зависимости 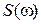 и
и 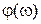 называют соответственно амплитудно-частотной и фазочастотной характеристиками ИП. Для ИП с линейной градуировочной характеристикой амплитудно-частотная и фазочастотная характеристики полностью характеризуют динамические свойства ИП при синусоидальном входном воздействии. Идеальной амплитудно-частотной характеристикой считается та, которая не зависит от частоты, т. е.
называют соответственно амплитудно-частотной и фазочастотной характеристиками ИП. Для ИП с линейной градуировочной характеристикой амплитудно-частотная и фазочастотная характеристики полностью характеризуют динамические свойства ИП при синусоидальном входном воздействии. Идеальной амплитудно-частотной характеристикой считается та, которая не зависит от частоты, т. е. 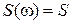 , где
, где 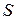 – статическая чувствительность ИП (см. 1.3.1).
– статическая чувствительность ИП (см. 1.3.1).
Динамические свойства ИП часто оценивают по рабочей полосе частот. При этом предельные частоты определяются по допустимому спаду амплитудно-частотной характеристики (АЧХ), задаваемый на уровне 0,707 или 0,9 от номинального значения. Для ИП, работающих как в статическом, так и в динамическом режимах, АЧХ имеет вид амплитудно-частотной характеристики фильтра нижних частот, имеющей одну граничную частоту сверху, а для ИП, работающих только в динамическом режиме, АЧХ имеет вид амплитудно-частотной характеристики полосового фильтра, имеющего две граничные частоты: снизу и сверху.
Комплексная динамическая чувствительность представляет собой частное решение дифференциального уравнения и определяет установившийся процесс при подаче на вход ИП синусоидального воздействия [8].
Решение дифференциального уравнения, как известно, можно искать также в операторной форме, позволяющей определить динамическую чувствительность при любом входном воздействии. Динамическая чувствительность или передаточная функция ИП в операторной форме находится по формуле
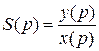 .
.
Частным случаем передаточной функции является переходная характеристика, представляющая собой временную зависимость выходного сигнала при скачкообразном изменении входного сигнала.
Характеристики динамических звеньев, представляющих наиболее распространенные ИП, представлены в таблице [8].
Таким образом, очевидно, что любой реальный ИП не может мгновенно реагировать на изменение входной величины и возникает динамическая погрешность, определение которой дано в 1.3.1. В этом определении подчеркивается, что погрешность в динамическом режиме всегда содержит также и статическую погрешность 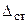 .
.
| Передаточная функция | Тип динамического звена | Уравнение в операторной форме |  Вид переходной характеристики Вид переходной характеристики
| Примеры ИП |
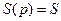
| Идеальное |
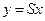
| — | |
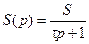
| Апериодическое |
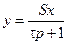
| 
| Термопары, терморезисторы |
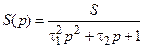
| Колебательное |
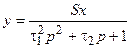
| 
| Струнные, магнитоупругие |
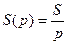
| Интегрирующее |
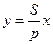
|

| Термопары и терморезисторы при синусоидальном входном сигнале |
а) 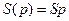 б)
б) 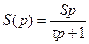
| Дифференцирующее а) идеальное б) реальное |
а) 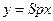 б)
б) 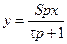
|
 а) б) а) б)
| Емкостные, индуктивные |
Появление динамической погрешности легко продемонстрировать на графике, иллюстрирующем переходный процесс при скачкообразном изменении входной величины 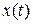 в предположении, что статическая погрешность отсутствует (рис. 1.3). В начальный момент
в предположении, что статическая погрешность отсутствует (рис. 1.3). В начальный момент 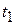 выходной параметр
выходной параметр 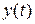 значительно отличается от установившегося значения
значительно отличается от установившегося значения 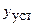 , которое он должен иметь в соответствии со значением
, которое он должен иметь в соответствии со значением 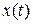 . Погрешность в динамическом режиме по выходной величине
. Погрешность в динамическом режиме по выходной величине 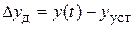 постепенно уменьшается и при
постепенно уменьшается и при 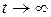
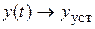 , а
, а 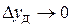 . Таким образом, если величина
. Таким образом, если величина 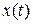 после скачка остается неизменной, достаточно выждать некоторое время τ и получить неискаженное значение
после скачка остается неизменной, достаточно выждать некоторое время τ и получить неискаженное значение 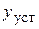 . Это время называется временем установления выходного сигнала ИП и является частной динамической характеристикой, которая часто нормируется и указывается в паспорте ИП. Очевидно, что время установления выходного сигнала ИП зависит от величины недохода
. Это время называется временем установления выходного сигнала ИП и является частной динамической характеристикой, которая часто нормируется и указывается в паспорте ИП. Очевидно, что время установления выходного сигнала ИП зависит от величины недохода 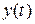 до
до 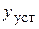 .
.
|
 В частности, в [9] это время называют постоянной времени и определяют на уровне 63 % от установившегося значения
В частности, в [9] это время называют постоянной времени и определяют на уровне 63 % от установившегося значения 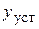 .
.
Если входная величина 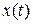 непрерывно изменяется во времени, то установившееся значение
непрерывно изменяется во времени, то установившееся значение 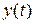 также зависит от времени и динамическая погрешность всегда присутствует. В этом случае
также зависит от времени и динамическая погрешность всегда присутствует. В этом случае 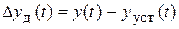 является мгновенным значением динамической погрешности выходной величины
является мгновенным значением динамической погрешности выходной величины
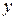 . Если предположить, что
. Если предположить, что 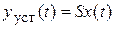 , то
, то 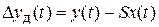 и абсолютная динамическая погрешность по входной величине определяется из выражения
и абсолютная динамическая погрешность по входной величине определяется из выражения
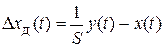 .
.
Сравнивая последнюю формулу с предыдущей, получим формулу для трансформации динамической погрешности с выхода на вход ИП и обратно:
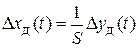 .
.
Соответственно могут быть найдены и относительные динамические погрешности как по входной, так и по выходной величинам.
 2020-05-25
2020-05-25 260
260








