Пример решения СЛАУ по алгоритму прогонки

23.04.2020

«Основы программирования: ЯП С/С++/С№»

Год обучения

Индивидуальная работа

Тема: Метод прогонки

Цель: познакомиться с методом прогонки

Задачи обучающие:

· познакомиться с методом прогонки при решении системы уравнений

· реализация очереди средствами С#;

· систематизировать знания обучающихся по данной теме;

· закрепить знания, полученные на предыдущих уроках;

Задачи развивающие:

· развивать умения использовать знания, полученные на уроках информатики, в учебной деятельности;

· развивать логическое мышление, умение обобщать, сопоставлять и применять полученные знания на практике;

· развивать познавательную деятельность обучающихся, развивать умение анализировать происходящие изменения в решении задач;

· развивать познавательный интерес, творческую активность, интеллект;

· развивать интуицию, эрудицию, самостоятельность в суждениях, упорство в достижении цели;

· формирование информационной культуры и потребности приобретения знаний;

· стимулирование познавательного интереса обучающихся по данной теме и дисциплине Информатика и ИКТ в целом.

Задачи воспитательные:

· воспитание творческого подхода к работе, желания экспериментировать;

· профессиональная ориентация и подготовка к трудовой деятельности;

· воспитание информационной культуры, самостоятельности, ответственности;

· развивать культуру общения, воспитывать внимание, сообразительность, находчивость.

ХОД УРОКА

Теория

Метод прогонки

https://habr.com/ru/post/418627/

Метод прогонки является частным случаем метода Гаусса. С помощью этого метода можно решать только специфические системы, имеющие не более трех неизвестных в каждой строке. То есть при системе

матрица A является трехдиагональной:

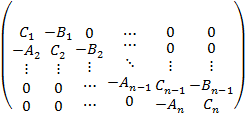
Сразу заметим, что имеется связь соседних решений:

— какие-то неизвестные числа. Если мы найдем их и какую-то одну переменную, то сможем найти и все остальные.

Вывод формул

присутствует здесь. Ну и в итоге

Отметим, что в формулах поиска присутствует деление на число , которое может оказаться нулем, что нужно отслеживать. Но на самом деле имеет место следующее утверждение, доказательство которого есть здесь: алгоритм прогонки является корректным и устойчивым, если выполняются условия: