Наибольшее распространение в настоящее время получили методы линейного программирования.
Основателем линейного программирования является советский математик Л. В. Канторович. В 1939 г. он опубликовал обстоятельную монографию «Математические методы организации и планирования производства», в которой впервые обосновал возможность количественного решения оптимальных планово-производственных задач.
Модель задачи линейного программирования (ЗЛП) должна иметь вполне определенный вид: требуется найти максимум (минимум) значения целевой функции L при переменных х1,х2..., хn
L(X) =с1х1 + c2x2 +... + спхп® max, min (1)
- при соблюдении системы линейных ограничений
 a11x1 + a 12x2+…+ a1nxn=b1
a11x1 + a 12x2+…+ a1nxn=b1
a 21x1 + a 22x2+…+ a2n xn=b2 (2)
………………………………
a m1x1 + a m2x2+…+ amnxn=bm
-условие неотрицательности
x j³ 0; j=1,2,….,n (3)
Получили задачу линейного программирования (ЗЛП)
max L(x) = 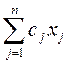
при ограничениях по ресурсам
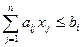 (i = 1, 2,……,m)
(i = 1, 2,……,m)
Функцию f(x1,x2, …,хn) принято называть целевой, т.к. её максимизация (минимизация) часто есть выражение какой-то цели, систему ограничений– специальными ограничениями ЗЛП, неравенства x1≥0,x≥02, …, хn≥0 – общими ограничениями ЗЛП. Множество всех допустимых решений ЗМП (хj≥0, j= 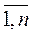 ) называется допустимым множеством этой задачи.
) называется допустимым множеством этой задачи.
При решении ЗЛП возможны следующие случаи:
1. задача имеет единственный оптимальный план;
2. задача имеет множество оптимальных планов;
3. линейная форма задачи не ограничена;
4. задача не имеет ни одного плана.
Если при решении задачи выполняется 2 и 3 условие, задача имеет множество допустимых решений. Если выполняются все три условия – задача имеет одно оптимальное решение.
При использовании ЗЛП в экономике:
xj- объем выпуска j -го вида продукции (искомая величина);
j - номер продукта;
n – общее количество различных видов продукции;
aij – норма расхода i -го ресурса на j— й продукт
i – номер ресурса;
m – общее количество ресурса;
bi – объем i -го вида ресурса;
сj - цена, прибыль, доход, себестоимость, затраты единицы j— го вида продукции
Общая постановка ЗЛП
Пусть на предприятии выпускается два вида продукции П1 и П2.
На производство этой продукции расходуется 4-е вида сырья: S1, S2, S3 и S4.
Запасы каждого вида сырья (ресурсы) ограничены и составляют соответственно: в1, в2, в3 и в4.
Норма расхода на производство единицы первого вида продукции П1:первого вида ресурса - а11; второго вида ресурса – а21; третьего вида ресурса – а31; четвертого вида ресурса – а41..
Норма расхода на производство единицы второго вида продукции П2:первого вида ресурса - а12; второго вида ресурса – а22; третьего вида ресурса – а32; четвертого вида ресурса – а42
Доход от реализации продукта П1 и П2. – с1 и с2.
Цель: определить какое количество продукции вида П1 и П2 необходимо выпустить предприятию, чтобы получить max доход.
Исходную информацию лучше всего записать в табличной форме.
| Вид ресурса | Вид продукции | Запас ресурса | |
| П1 | П2. | ||
| S1 | а11 | а12 | в1 |
| S2 | а21 | а22 | в2 |
| S3 | а31 | а32 | в3 |
| S4 | а41 | а42 | в4 |
| Доход | с1 | с2 |
Для составления ЗЛП введем неизвестные х1 - П1 и х2 - П2.
Составляем целевую функцию: L(X) =с1х1 + c2x2 ® max
Ограничительные уравнения (так как у нас четыре вида сырья, то и четыре ограничения): a11x1 + a 12x2 ≤b1
a21x1 + a 22x2≤b2
……………………
……………………
Знак ≤, так как сырье может быть израсходовано в количестве меньше имеющихсяресурсов или израсходовано полностью.
Условие неотрицательности: х1 ≥ 0 и х2 ≥ 0
 2014-02-02
2014-02-02 1407
1407








