2020-05-25
195
На рисунке изображён график некоторой функции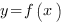 
. Функция 
— одна из первообразных функции 
. Найдите площадь закрашенной фигуры.
Закрашенная фигура представляет собой криволинейную трапецию, ограниченную сверху графиком функции 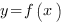, слева прямой 
, справа прямой 
, и снизу осью ОХ.
Площадь этой криволинейной трапеции вычисляется по формуле:
, где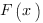 
- первообразная функции 
.
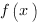По условию задачи , поэтому, чтобы найти площадь фигуры, нам нужно найти значение первообразной в точке -8, в точке -10, и затем из первого вычесть второе.
Замечу, что в этих задачах очень часто возникают ошибки именно в вычислениях, поэтому советую аккуратно и подробно их записывать, и ничего не считать "в уме".
= 
= 
Ответ: 4
