Задачи, о площади криволинейной трапеции

1 2

ВОПРОС 33

«ЭТАЛОННЫЕ РЯДЫ», ИСПОЛЬЗУЕМЫЕ ДЛЯ СРАВНЕНИЯ

Отметим эталонные ряды, часто используемые для сравнения:

1) Геометрический ряд 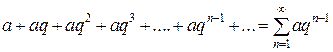, при 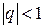- ряд сходится, при 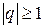- расходится.

2) Гармонический ряд 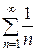- расходится

3) Обобщенный гармонический ряд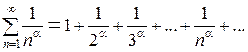

сходится при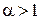

расходится при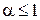

Трудность работы по 1 признаку сравнения, заключается в том, что нужно не только подобрать эталонный ряд, но и доказать, что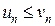

В ряде случаев эффективным оказывается применение 2 предельного признака сравнения.

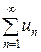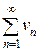ТЕОРЕМА: (2 предельный признак сравнения) Если (1) и (2)

– ряды с положительными членами и существует конечный предел отношения их общих членов 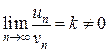, тогда ряды одновременно или сходятся, или расходятся.

ПРИМЕР: Исследовать сходимость ряда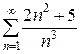

Сравним данный ряд с гармоническим рядом 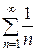, о котором точно известно, что он расходится. Почему будем сравнивать именно с ним?

Ответ: при 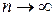: 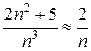, т.к. 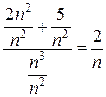, поэтому и будем сравнивать данный ряд с .

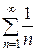Рассмотрим предел отношения общих членов ряда, согласно предельному признаку сравнения 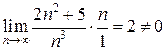; следовательно, делаем вывод, что данный ряд расходится, как и гармонический.

ТЕОРЕМА: (Признак ДАЛАМБЕРА) Пусть для ряда 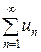с положительными членами существует предел отношения 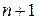- го члена к 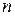- му члену, 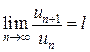, тогда если:

1. Если 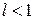, то ряд сходится

2. Если 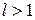, то ряд расходится

3. Если 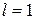, то вопрос о сходимости остается открытым.

Пример: Исследовать на сходимость ряд: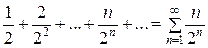

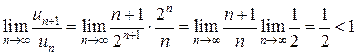
Следовательно, ряд сходится.

ВОПРОС 13

ЗАДАЧИ, О ПЛОЩАДИ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ

В этой статье мы будем учиться решать задачи на нахождение площади криволинейной трапеции.

Как всегда, начнем с теории. Как вы помните, неопределенный интеграл от функции 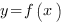- это множество всех первообразных :

∫

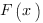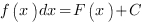
В неопределенном интеграле не заданы границы интегрирования, и в результате нахождения неопределенного интеграла от функции 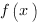мы получаем множество первообразных, отличающихся друг от друга на постоянную величину С.

Если заданы границы интегрирования, то мы получаем определенный интеграл:

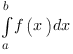
Здесь число 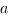- нижний предел интегрирования, число 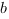- верхний предел интегрирования. Определенный интеграл - это ЧИСЛО, значение которого вычисляется по формуле Ньютона - Лейбница:

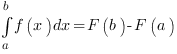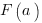- это значение первообразной функции 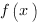в точке 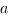, и, соответственно, 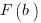- это значение первообразной функции 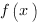в точке .

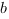Для нас с точки зрения решения задач важное значение имеет геометрический смысл определенного интеграла.

Рассмотрим фигуру, изображенную на рисунке:

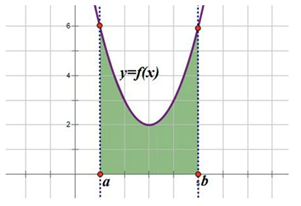
Зеленая фигура, ограниченая сверху графиком функции 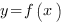, слева прямой 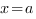, справа прямой 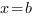, и снизу осью ОХ называется криволинейной трапецией.

Геометрический смысл определенного интеграла:

Определенный интеграл 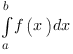- это число, равное площади криволинейной трапеции - фигуры, ограниченой сверху графиком положительной на отрезке 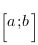функции 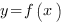, слева прямой 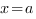, справа прямой 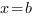, и снизу осью ОХ.