ПРАКТИЧЕСКАЯ РАБОТА
СФЕРА. УРАВНЕНИЕ СФЕРЫ.
Цель: закрепить навыки решения практических задач на применение уравнения сферы.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
СФЕРА .
Определение:Сферой называется поверхность, состоящая из всех точек пространства, которые расположены на данном расстоянии от данной точки.
Основные элементы:

Рис. 1.
Данная точка – центр сферы.
Данное расстояние – радиус сферы.
Радиус сферы – любой отрезок, соединяющий центр и какую-нибудь точку сферы.
Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы равен 2R.
Сфера может быть получена вращением полуокружности вокруг ее диаметра.
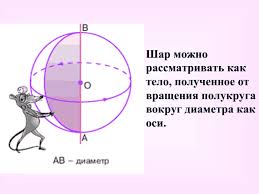
Рис. 2.
Уравнение сферы:
Зададим прямоугольную систему координат Oxyz. Построим сферу с центром в точке  с радиусом R. Точка
с радиусом R. Точка 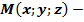 произвольная точка сферы.
произвольная точка сферы.
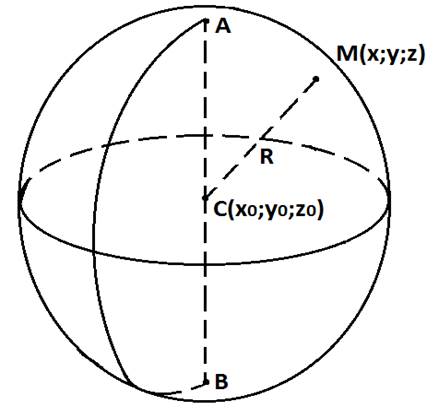
Рис. 3.
Расстояние между двумя точками:  . Допустим, что МС = R, возведя правую и левую части в квадрат, получим в прямоугольной системе координат уравнение сферы радиуса R с центром
. Допустим, что МС = R, возведя правую и левую части в квадрат, получим в прямоугольной системе координат уравнение сферы радиуса R с центром  :
:


|
| ||||
|
|
| |||
ОБРАЗЕЦ ВЫПОЛНЕНИЯ УПРАЖНЕНИЙ
1. Напишите уравнение сферы радиуса R с центром А, если:
а) А(2; -4;7), R = 3;
б) А(0;0;0), R = 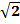 ;
;
в) А(2;0;0), R = 4;
| Дано: | Решение: |
а) А(2; -4;7), R = 3;
б) А(0;0;0), R = 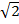 ;
в) А(2;0;0), R = 4. ;
в) А(2;0;0), R = 4.
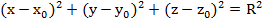
| Уравнение сферы:
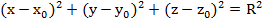 а)
а) 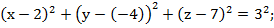
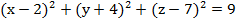 б)
б) 
 в)
в) 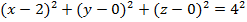
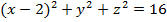
|
| Ответ: а) б) в) | |
2. Найдите координаты центра и радиус сферы, заданной уравнением:
а) 
б) 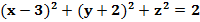
| Дано: | Решение: |
а) 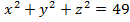 б)
б) 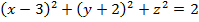
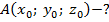 R -?
R -?
| Уравнение сферы:
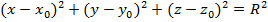 а)
а) 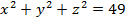 А(0; 0; 0), т.к. координаты
А(0; 0; 0), т.к. координаты 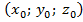 отсутствуют в данном выражении. отсутствуют в данном выражении.
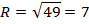
 А(3; -2; 0),
А(3; -2; 0), 
|
Ответ: А(3; -2; 0), 
|
3. Напишите уравнение сферы с центром А, проходящей через точку N, если:
а) А(-2; 2; 0), N(0; 0; 0)
б) А(-2; 2; 0), N(5; 0; 1)
| Дано: | Решение: |
а) А(-2; 2; 0), N(0; 0; 0)
б) А(-2; 2; 0), N(5; 0; 1)
в) А(0; 0; 0), N(5; 3; 1)
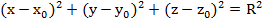 R -?
R -?
| Радиус R будет равен расстоянию между двумя точками – А( 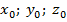 ) и N( ) и N( 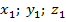 ). ).
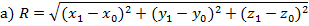
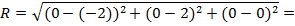
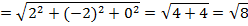 Уравнение сферы:
Уравнение сферы: 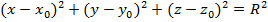 , где , где
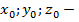 координаты точки центра сферы – координаты точка А( координаты точки центра сферы – координаты точка А( 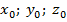 ). ).
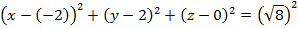
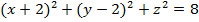


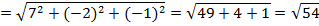 Уравнение сферы:
Уравнение сферы: 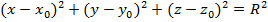 , где , где
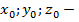 координаты точки центра сферы – координаты точка А( координаты точки центра сферы – координаты точка А( 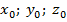 ). ).

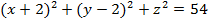
|
| Ответ:
| |
Самостоятельная работа
1. Напишите уравнение сферы радиуса R с центром А, если:
а) А(3; -2; 1) и R = 7 дм;
б) А(0; 0; 2) и R = 5 м.
2. Найдите координаты центра точки Аи радиус сферы, заданной уравнением:
а) 
б) 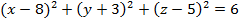
3. Напишите уравнение сферы с центром А, проходящей через точку N, если А(7; 6; -5) и N(2; -3; 8).
Критерии:
| Отметка | Число заданий, необходимое для получения отметки |
| «5» (отлично) | 3 |
| «4» (хорошо) | 2 |
| «3» (удовлетворительно) | 1 |
 2020-05-25
2020-05-25 204
204


 ;
; 






